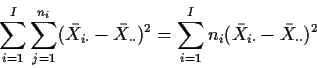Postscript version of these notes
Reading: Chapter 5, Chapter 6 sections 1-5, Chapter 7 sections 1-3.
STAT 350: Lecture 4
The Geometry of Least Squares
Mathematical Basics
- Inner / dot product: a and b column vectors
- Matrix Product: A is
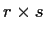 B is
B is
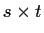
Partitioned Matrices
Partitioned matrices are like ordinary matrices but the entries
are matrices themselves. They add and multiply (if the dimensions match
properly) just like regular matrices but(!) you must remember that
matrix multiplication is not commutative. Here is an example
You can think of A as a
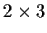 matrix and B as a
matrix and B as a
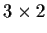 matrix
and then multiply them to get C=AB a
matrix
and then multiply them to get C=AB a
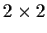 matrix as follows:
matrix as follows:
BUT: this only works if each of the matrix products in
the formulas makes sense. So, A11 must have the same number
of columns as B11 has rows and many other similar restrictions
apply.
First application:
where each Xi is a column of X.
Then
which is a linear combination of the columns of X.
Definition: The column space of X, written
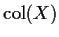 is the
(vector space of) set of all linear combinations of columns of X also called the
space ``spanned'' by the columns of X.
is the
(vector space of) set of all linear combinations of columns of X also called the
space ``spanned'' by the columns of X.
SO:
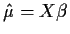 is in
is in
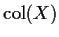 .
.
Back to normal equations:
or
or
or
or
Definition:
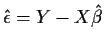 is the fitted
residual vector.
is the fitted
residual vector.
SO:
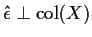 and
and
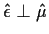
Pythagoras' Theorem: If 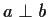 then
then
||a||2 + ||b||2 = ||a+b||2
Definition: ||a|| is the ``length'' or ``norm'' of a:
Moreover, if
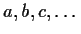 are all perpendicular then
are all perpendicular then
Application:
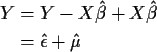
so
or
Definitions:
We have several alternative formulas for the Regression SS:
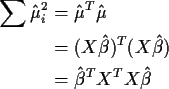
(Notice the matrix identity which I will use regularly:
(AB)T = BT AT.)
What is least squares
Choose 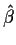 to minimize
to minimize
That is, to minimize
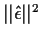 .
The resulting
.
The resulting 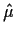 is called the Orthogonal Projection
of Y onto the column space of X.
is called the Orthogonal Projection
of Y onto the column space of X.
Extension:
Imagine we fit 2 models:
- 1.
- The FULL model:
- 2.
- The REDUCED model:
If we fit the full model we get
 |
(1) |
If we fit the reduced model we get
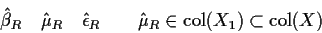 |
(2) |
Notice that
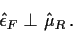 |
(3) |
(The vector 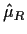 is in the column space of X1 so it is in the column space of X and
is in the column space of X1 so it is in the column space of X and
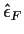 is orthogonal to everything in the column space of X.)
So:
is orthogonal to everything in the column space of X.)
So:
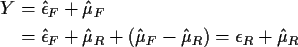
You know
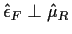 (from (3) above) and
(from (3) above) and
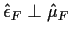 (from (1) above). So
(from (1) above). So
Also
So
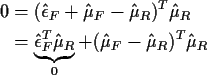
so
Summary:
where all three vectors on the Right Hand Side are perpendicular to
each other.
This gives:
which is an Analysis of Variance (ANOVA) table!
Here is the most basic version of the above:
The notation here is that
is a column vector with all entries equal to 1. The coefficient of this
column, 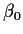 ,
is called the ``intercept'' term in the model.
,
is called the ``intercept'' term in the model.
To find 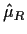 we minimize
we minimize
and get simply
and
Our ANOVA identity is now
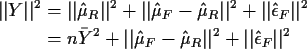
This identity is usually rewritten in subtracted form:
Remembering the identity
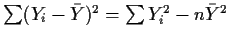 we find
we find
These terms are respectively the Adjusted or Corrected Total Sum of Squares,
the Regression or Model Sum of Squares and the Error Sum of Squares.
The sum of squares decomposition in one example
See
Lecture 2
for more about this example. There I showed the design matrix for the
model
with
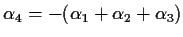 .
.
The data consist of blood coagulation times for 24 animals
fed one of 4 different diets.
In the following I write the data in a table and decompose
the table into a sum of several tables. The 4 columns of
the table correspond to Diets A, B, C and D. You should think
of the entries in each table as being stacked up into
a column vector, but the tables save space.
The design matrix can be partitioned into a column of 1s and
3 other columns. You should compute the product XTX and get
The matrix XTY is just
The matrix XTX can be inverted using a program like Maple.
I found
that
It now takes quite a bit of algebra to verify that the vector of
fitted values can be computed by simply averaging the data in each column.
That is, the fitted value, 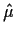 is the table
is the table
On the other hand fitting the model with a design matrix
consisting only of a column of 1s just leads to 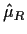 (notation from the lecture) given by
(notation from the lecture) given by
Now in class I gave the decomposition
which corresponds to the following identity:
The sums of squares of the entries of each of these arrays are
as follows.
On the left hand side
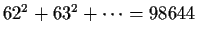 .
This is the
uncorrected total sum of squares. The first term
on the right hand side gives
24(642) = 98304. This term
is sometimes put in ANOVA tables as the Sum of Squares due to the
Grand Mean but it is usually subtracted from the total to produce the
Total Sum of Squares we usually put at the bottom of the table
and often called the Corrected (or Adjusted) Total Sum of Squares.
In this case the corrected sum of squares is the squared
length of the table
.
This is the
uncorrected total sum of squares. The first term
on the right hand side gives
24(642) = 98304. This term
is sometimes put in ANOVA tables as the Sum of Squares due to the
Grand Mean but it is usually subtracted from the total to produce the
Total Sum of Squares we usually put at the bottom of the table
and often called the Corrected (or Adjusted) Total Sum of Squares.
In this case the corrected sum of squares is the squared
length of the table
which is 340.
The second term on the right hand side of the equation has squared length
4(-3)2 + 6(2)2 + 6 (4)2 + 8 (-3)2 = 228 (which is the Treatment
Sum of Squares produced by SAS). The formula for this Sum of Squares is
but I want you to see that the formula is
just the squared length of the vector of individual sample means minus
the grand mean. The last vector of the decomposition is called
the residual vector and has squared length
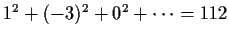 .
Corresponding to the decomposition of the total squared length
of the data vector is a decomposition of its dimension, 24, into the
dimensions of subspaces. For instance the grand mean is always a multiple
of the single vector all of whose entries are 1; this describes
a one dimensional space (this is just another way of saying that the
reduced
.
Corresponding to the decomposition of the total squared length
of the data vector is a decomposition of its dimension, 24, into the
dimensions of subspaces. For instance the grand mean is always a multiple
of the single vector all of whose entries are 1; this describes
a one dimensional space (this is just another way of saying that the
reduced 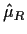 is in the column space of the reduced model design
matrix). The second vector, of deviations from a grand
mean lies in the three dimensional subspace of tables which are constant
in each column and have a total equal to 0. Similarly the vector of
residuals lies in a 20 dimensional subspace - the set of all tables whose
columns sum to 0. This decomposition of dimensions is the decomposition
of degrees of freedom. So
24 = 1+3+20 and the degrees of freedom for
treatment and error are 3 and 20 respectively. The vector whose squared
length is the Corrected Total Sum of Squares lies in the 23 dimensional
subspace of vectors whose entries sum to 1; this produces the 23 total
degrees of freedom in the usual ANOVA table.
is in the column space of the reduced model design
matrix). The second vector, of deviations from a grand
mean lies in the three dimensional subspace of tables which are constant
in each column and have a total equal to 0. Similarly the vector of
residuals lies in a 20 dimensional subspace - the set of all tables whose
columns sum to 0. This decomposition of dimensions is the decomposition
of degrees of freedom. So
24 = 1+3+20 and the degrees of freedom for
treatment and error are 3 and 20 respectively. The vector whose squared
length is the Corrected Total Sum of Squares lies in the 23 dimensional
subspace of vectors whose entries sum to 1; this produces the 23 total
degrees of freedom in the usual ANOVA table.



Richard Lockhart
1999-01-11
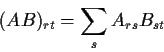
![\begin{displaymath}A = \left[\begin{array}{c\vert c\vert c}
A_{11} & A_{12} & A_{13}
\\
\hline
A_{21} & A_{22} & A_{23}
\end{array} \right]
\end{displaymath}](img7.gif)
![\begin{displaymath}B = \left[\begin{array}{c\vert c}
B_{11} & B_{12}
\\
\hline
B_{21} & B_{22}
\\
\hline
B_{31} & B_{32}
\end{array} \right]
\end{displaymath}](img8.gif)
![\begin{displaymath}AB =
\left[\begin{array}{c\vert c}
A_{11}B_{11} + A_{12}B_{...
...A_{21}B_{12} + A_{22}B_{22} + A_{23}B_{32}
\end{array} \right]
\end{displaymath}](img12.gif)
![\begin{displaymath}X\beta = \left[ X_1 \vert X_2 \vert \cdots \vert X_p \right]
...
...ray}\right] =
X_1 \beta_1 + X_2 \beta_2 + \cdots + X_p \beta_p
\end{displaymath}](img14.gif)
![]() is the
(vector space of) set of all linear combinations of columns of X also called the
space ``spanned'' by the columns of X.
is the
(vector space of) set of all linear combinations of columns of X also called the
space ``spanned'' by the columns of X.
![]() is in
is in
![]() .
.
![\begin{displaymath}\left[\begin{array}{c} X_1^T \\ \vdots \\ X_p^T \end{array}\right]
\left[ Y-X\hat\beta\right] = 0
\end{displaymath}](img19.gif)
![]() is the fitted
residual vector.
is the fitted
residual vector.
![]() and
and
![]()
![]() then
then
![]() are all perpendicular then
are all perpendicular then
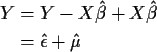
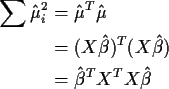
![]() to minimize
to minimize
![\begin{displaymath}X= \left[ X_1 \vert X_2 \right] \quad
\beta = \left[ \begin{...
... \beta_1 \\ \hline \beta_2 \end{array} \right]
\quad p=p_1+p_2
\end{displaymath}](img40.gif)
![]() (from (3) above) and
(from (3) above) and
![]() (from (1) above). So
(from (1) above). So
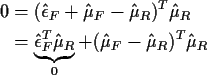
![\begin{displaymath}{\bf 1} = \left[ \begin{array}{c} 1 \\ \vdots \\ 1 \end{array} \right]
\end{displaymath}](img58.gif)
![]() we minimize
we minimize
![\begin{displaymath}\hat\mu_R = \left[
\begin{array}{c} \bar{Y} \\ \vdots \\ \bar{Y} \end{array} \right]
\end{displaymath}](img62.gif)
![\begin{displaymath}\left[
\begin{array}{rrrr}
24 & -4 & -2 & -2 \\
-4 & 12 & ...
... \\
-2 & 8 & 14 & 8 \\
-2 & 8 & 8 & 14
\end{array}\right]
\end{displaymath}](img69.gif)
![\begin{displaymath}\left[ \sum_{ij} Y_{ij}\, , \, \sum_j Y_{1j} - \sum_j Y_{4j}
...
...j} - \sum_j Y_{4j}\, , \, \sum_j Y_{3j} - \sum_j
Y_{4j}\right]
\end{displaymath}](img70.gif)
![\begin{displaymath}384 (X^TX)^{-1} = \left[
\begin{array}{rrrr}
17 & 7 & -1 & -...
...1 & -23 & 49 & -15 \\
-1 & -23 & -15 & 49
\end{array}\right]
\end{displaymath}](img71.gif)
![\begin{displaymath}\left[
\begin{array}{rrrr}
61 & 66 & 68 & 61 \\
61 & 66 & ...
... & 66 & 68 & 61 \\
& & & 61 \\
& & & 61
\end{array}\right]
\end{displaymath}](img72.gif)
![\begin{displaymath}\left[
\begin{array}{rrrr}
64 & 64 & 64 & 64 \\
64 & 64 & ...
... & 64 & 64 & 64 \\
& & & 64 \\
& & & 64
\end{array}\right]
\end{displaymath}](img73.gif)
![\begin{displaymath}\left[
\begin{array}{rrrr}
62 & 63 & 68 & 56 \\
60 & 67 & ...
...\\
& 0 & 0 & 3 \\
& & & 2 \\
& & & -2
\end{array}\right]
\end{displaymath}](img74.gif)
![]() .
This is the
uncorrected total sum of squares. The first term
on the right hand side gives
24(642) = 98304. This term
is sometimes put in ANOVA tables as the Sum of Squares due to the
Grand Mean but it is usually subtracted from the total to produce the
Total Sum of Squares we usually put at the bottom of the table
and often called the Corrected (or Adjusted) Total Sum of Squares.
In this case the corrected sum of squares is the squared
length of the table
.
This is the
uncorrected total sum of squares. The first term
on the right hand side gives
24(642) = 98304. This term
is sometimes put in ANOVA tables as the Sum of Squares due to the
Grand Mean but it is usually subtracted from the total to produce the
Total Sum of Squares we usually put at the bottom of the table
and often called the Corrected (or Adjusted) Total Sum of Squares.
In this case the corrected sum of squares is the squared
length of the table
![\begin{displaymath}\left[
\begin{array}{rrrr}
-2 & -1 & 4 & -8 \\
-4 & 3 & 2 ...
...\
& 2 & 4 & 0 \\
& & & -1 \\
& & & -5
\end{array}\right]
\end{displaymath}](img76.gif)