


Postscript version of these notes
STAT 350 Lecture 2
Reading: Chapter 5 sections 1-4.
Matrix form of a linear model
Stack Yi, 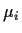 and
and
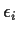 into vectors:
into vectors:
Define
Note
so
Finally
is our original set of n model equations written in vector matrix form.
Assumptions so far:
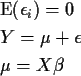
Still to come: independence, homoscedasticity, normality.
Examples: please take the point that this is a very large class
of models.
- 1.
- One sample problem:
-
 measured under ``identical'' conditions.
measured under ``identical'' conditions.
- So
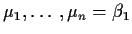 ,
say.
,
say.
-
![$X = \left[ \begin{array}{c}1 \\ 1 \\ \vdots \\ 1 \end{array}\right]_{n \times 1}
$](img11.gif)
-
![$\beta = \left[\beta_1 \right]_{1 \times 1}$](img12.gif) (so p=1).
(so p=1).
-
![$Y= \left[ \begin{array}{c}1 \\ 1 \\ \vdots \\ 1 \end{array}\right]\beta +\epsilon$](img13.gif) .
.
- 2.
- Two sample problem: n=r+s
For 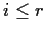
For
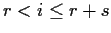
In matrix form
Sometimes it is convenient to write:
which is a partitioned matrix where I have described the transpose of X.
- 3.
- Simple linear regression:
Yi = TL
Di = Dose
The model
gives
- 4.
- Polynomial models: ``polynomial regression''. In
Lecture 1
we had the quadratic model:
for which
In general we might fit a polynomial of degree p-1 to get
for which
- 5.
- Analysis of Covariance: fitting two straight lines
Consider the TL data again but now suppose that samples
1 to r were ``bleached'' (left in the sun for several
hours before analysis) and samples r+1 to s were
``unbleached''. We combine the 2 sample problem with the
straight line problem:
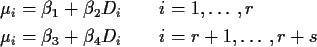
Special case: ``No interaction'' of Bleach and Dose:
the effect of dose is the same
for bleached and unbleached samples. That is:
Note: we usually re-order the parameters in this case to get
- 6.
- Weighing designs: (a simple example mostly for illustration)
Idea: weigh two objects with (true) weights
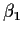 and
and 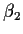 .
.

Now we have
and get
so that
Notice that
 is a physically
meaningful and important assumption. This sort of assumption
may well be wrong.
is a physically
meaningful and important assumption. This sort of assumption
may well be wrong.
- 7.
- One way layout (ANOVA). Example has data Yij being
the blood coagulation time for rat number j fed diet number i
for i=1,2,3,4. There were 4 rats for diet 1, 6 for diets 2 and 3
and 8 rats fed diet 4. We use
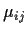 as notation for
as notation for
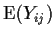 .
The idea is that all the rats fed diet 1 have the same mean coagulation
time
.
The idea is that all the rats fed diet 1 have the same mean coagulation
time 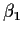 so
so
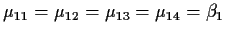 .
(In fact it is pretty common notation to use
.
(In fact it is pretty common notation to use 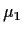 for
for 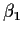 but
this will conflict, for the time being, with my notation for the mean of
the first Y.)
If we stack up the Ys we get
but
this will conflict, for the time being, with my notation for the mean of
the first Y.)
If we stack up the Ys we get
Again we have
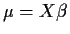 .
.
Jargon: X is called a ``design matrix''.
The one way layout as a linear model
The sum of squares decomposition in one example
The data consist of blood coagulation times for 24 animals
fed one of 4 different diets. Here are the data with the 4 diets
being the 4 columns.
The usual ANOVA model equation is
which we can write in matrix form by stacking up the
observations into a column.
Let X denote the
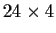 design matrix in this formula.
Usually we reparametrize the model in the form
design matrix in this formula.
Usually we reparametrize the model in the form
which would lead to a design matrix which looked like X above with an
extra column on the left all of whose entries are equal to 1. The parameter vector
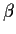 would now be
would now be
It will turn out that trying to use this parametrization the different parameters
are not identifiable, that is, they cannot be separately estimated, because making
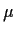 bigger by a certain amount and each
bigger by a certain amount and each 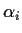 smaller by the same amount leaves
the data unchanged. We usually solve this problem by defining
smaller by the same amount leaves
the data unchanged. We usually solve this problem by defining
and
Now it is automatic
that
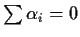 so we usually eliminate
so we usually eliminate 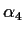 by replacing it in the
model equation by the quantity
by replacing it in the
model equation by the quantity
This leads to
and
Further analysis of this data.



Richard Lockhart
1999-01-12
![]() and
and
![]() into vectors:
into vectors:
![\begin{displaymath}\begin{array}{ccc}
Y = \left[ \begin{array}{c} Y_1 \\ Y_2 \\ ...
...silon_2 \\ \vdots \\ \epsilon_n \end{array} \right]
\end{array}\end{displaymath}](img3.gif)
![\begin{displaymath}\begin{array}{cc}
\beta = \left[ \begin{array}{c} \beta_1 \\ ...
... & \cdots & x_{n,p} \end{array} \right]_{n\times p}
\end{array}\end{displaymath}](img4.gif)
![\begin{displaymath}X\beta = \left[ \begin{array}{c}
x_{1,1} \beta_1 + \cdots + x...
...1} \beta_1 + \cdots + x_{n,p} \beta_p
\end{array} \right]
=\mu
\end{displaymath}](img5.gif)
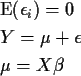
![$X = \left[ \begin{array}{c}1 \\ 1 \\ \vdots \\ 1 \end{array}\right]_{n \times 1}
$](img11.gif)
![$Y= \left[ \begin{array}{c}1 \\ 1 \\ \vdots \\ 1 \end{array}\right]\beta +\epsilon$](img13.gif) .
.
![\begin{displaymath}Y = \left[ \begin{array}{cc}
1 & 0 \\ \vdots & \vdots \\ 1 &...
...gin{array}{c} \beta_1 \\ \beta_2 \end{array}\right] + \epsilon
\end{displaymath}](img20.gif)
![\begin{displaymath}X^T = \left[ \overbrace{
\begin{array}{ccc} 1 & \cdots & 1 \...
... & 0 \\ 1 & \cdots & 1 \end{array}}^{s \mathrm{\ cols}}\right]
\end{displaymath}](img21.gif)
![\begin{displaymath}\beta=\left[\begin{array}{c} \beta_1 \\ \beta_2 \end{array}\r...
...c}
1 & D_1 \\
\vdots & \vdots \\
1 & D_n
\end{array}\right]
\end{displaymath}](img23.gif)
![\begin{displaymath}\beta=\left[\begin{array}{c} \beta_1 \\ \beta_2 \\ \beta_3 \e...
...ts & D_n \\
D_1^2 & D_2^2 & \cdots & D_n^2 \end{array}\right]
\end{displaymath}](img25.gif)
![\begin{displaymath}\beta=\left[\begin{array}{c} \beta_1 \\ \vdots \\ \beta_p \en...
...
D_1^{p-1} & D_2^{p-1} & \cdots & D_n^{p-1} \end{array}\right]
\end{displaymath}](img27.gif)
![]()
![\begin{displaymath}\beta = \left[\begin{array}{c} \beta_1 \\ \beta_2 \\ \beta_3 \\ \beta_4
\end{array}\right]
\end{displaymath}](img29.gif)
![\begin{displaymath}X^T = \left[ \begin{array}{ccc} 1 & \cdots & 1 \\
D_1 & \cdo...
... \\
1 & \cdots & 1 \\
D_1 & \cdots & D_r
\end{array} \right]
\end{displaymath}](img30.gif)
![\begin{displaymath}\beta = \left[\begin{array}{c} \beta_1 \\ \beta_2 \\ \beta_3
\end{array}\right]
\end{displaymath}](img32.gif)
![\begin{displaymath}X^T = \left[ \begin{array}{ccc} 1 & \cdots & 1 \\
D_1 & \cdo...
...\\
D_1 & \cdots & D_r \\
1 & \cdots & 1
\end{array} \right]
\end{displaymath}](img33.gif)
![\begin{displaymath}\beta = \left[\begin{array}{c} \beta_1 \\ \beta_3 \\ \beta_2
\end{array}\right]
\end{displaymath}](img34.gif)
![\begin{displaymath}X^T = \left[ \begin{array}{ccc} 1 & \cdots & 1 \\
0 & \cdots...
...\\
1 & \cdots & 1 \\
D_1 & \cdots & D_r
\end{array} \right]
\end{displaymath}](img35.gif)

![\begin{displaymath}\left[ \begin{array}{c} \mu_1 \\ \mu_2 \\ \mu_3 \end{array} \...
...\left[ \begin{array}{c}
\beta_1 \\ \beta_2 \end{array} \right]
\end{displaymath}](img40.gif)
![\begin{displaymath}X = \left[ \begin{array}{cc}
1 & 0
\\
0 & 1
\\
1 & 1
\end{array} \right]
\end{displaymath}](img41.gif)
![\begin{displaymath}Y =
\left[
\begin{array}{c}
Y_{11} \\ Y_{12} \\ Y_{13} \\ Y_...
...1} \\ \beta_{2} \\ \beta_{3} \\ \beta_{4}
\end{array} \right]
\end{displaymath}](img47.gif)
![\begin{displaymath}\left[
\begin{array}{rrrr}
62 & 63 & 68 & 56 \\
60 & 67 & ...
... & 66 & 68 & 64 \\
& & & 63 \\
& & & 59
\end{array}\right]
\end{displaymath}](img49.gif)
![\begin{displaymath}\left[\begin{array}{r}
62 \\
60 \\
63 \\
59 \\
63 \\
67 ...
...n_{46} \\
\epsilon_{47} \\
\epsilon_{48}
\end{array}\right]
\end{displaymath}](img51.gif)
![\begin{displaymath}X =
\left[
\begin{array}{rrrr}
1 & 1 & 0 & 0 \\
1 & 1 & 0 & ...
... \\
1 & -1 & -1 & -1 \\
1 & -1 & -1 & -1
\end{array}\right]
\end{displaymath}](img64.gif)