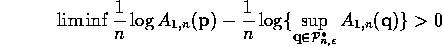
We have now reduced the proof of theorem 3 to that of establishing
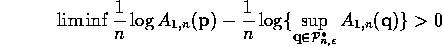
almost surely. We will prove this by establishing
almost surely and
almost surely.
To prove 9 note that 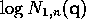 differs from
differs from
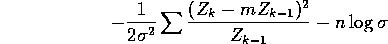
by a constant not depending on 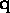 (note that we suppress the
dependence
of
(note that we suppress the
dependence
of 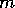 and
and 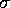 on
on 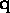 ). For fixed
). For fixed 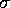 this is maximized
as a
function of
this is maximized
as a
function of 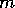 by
by 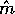 . The profile obtained by replacing
. The profile obtained by replacing 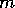 by
by
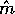 is concave and is maximized over all
is concave and is maximized over all 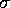 by
by 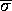 .
Since
this estimate is strongly consistent on the explosion set, the profile
is
maximized, subject to
.
Since
this estimate is strongly consistent on the explosion set, the profile
is
maximized, subject to 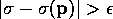 at one of
the two
points
at one of
the two
points 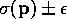 . Finally, 9 is
easily established by considering the two values
. Finally, 9 is
easily established by considering the two values 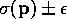 individually.
individually.
Fix  and let
and let 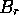 be the event that
be the event that  for
all
for
all 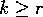 . Then
. Then 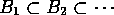 and
and 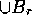 is the explosion
set except for a
is the explosion
set except for a 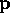 -null event. For trajectories in
-null event. For trajectories in 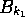 with
with
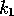 chosen large we write
chosen large we write
We will choose 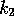 and
and 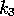 depending on
depending on 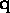 . In particular
let
. In particular
let
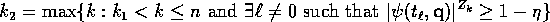
with 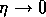 to be chosen later and
to be chosen later and
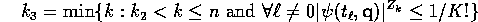
Each  is a probability so bounded by 1. Thus
is a probability so bounded by 1. Thus
The first term in 12 is free of 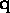 and after
division by
and after
division by  converges to 0 almost
surely on
converges to 0 almost
surely on 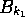 . Also on
. Also on 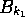
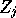 grows exponentially
when
grows exponentially
when  and so
and so
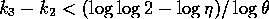 . From 1
we obtain
. From 1
we obtain
On 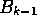 we have
we have 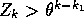 . Thus, except for a fixed number of
. Thus, except for a fixed number of 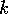 (depending only on
(depending only on 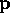 and
and 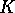 ) the right hand side of 13 is less than
) the right hand side of 13 is less than 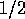 permitting a Taylor expansion of the
permitting a Taylor expansion of the 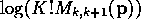 . Hence
. Hence
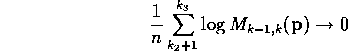
almost surely.
For the fourth term in 12 we have
for all  . Letting
. Letting 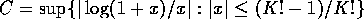 a Taylor expansion of the logarithm then shows that
a Taylor expansion of the logarithm then shows that
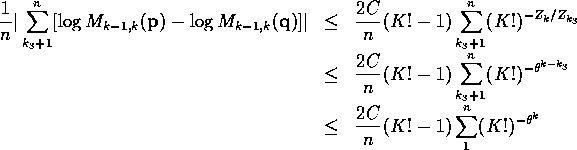
which converges to 0 almost surely.
It remains to deal with the second term in 12.
This
is
the most technical part of the argument.
Consider now any 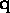 for which
for which 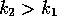 . (Remember that
. (Remember that
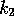 depends on
depends on 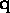 .) There is an
.) There is an 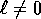 for which
for which
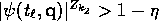 . There is then a constant
. There is then a constant 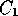 not
depending
on
not
depending
on 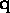 or
or 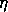 such that for all small
such that for all small 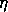
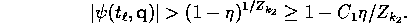
Since 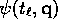 is in the convex hull of the points
is in the convex hull of the points 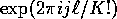 as
as 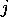 runs over
runs over 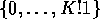 and since this convex
hull is a regular polygon there is a constant
and since this convex
hull is a regular polygon there is a constant 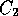 depending only on
depending only on
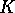 such that there must exist an
such that there must exist an  with
with
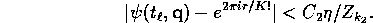
Finally there is a 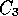 depending only on
depending only on 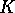 such that
such that
Let 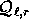 be the set of all
be the set of all 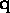 such that 15
holds. Note that either
such that 15
holds. Note that either 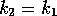 and the second term above is 0 or
and the second term above is 0 or
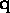 belongs to some
belongs to some 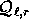 . For
. For 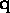 in
in 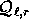 and
and 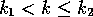 we have
we have
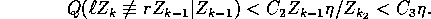
Let
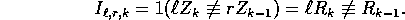
Then
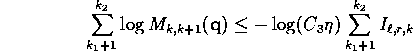
An argument like that at (14)
shows that the sequence 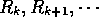 is asymptotically
an iid sequence of uniformly distributed random variables. Using this argument we can establish
is asymptotically
an iid sequence of uniformly distributed random variables. Using this argument we can establish
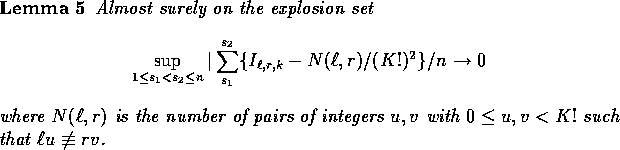
Since 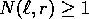 we can choose
we can choose 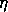 so that
so that
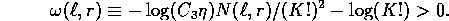
With this choice of 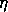 we can use the lemma to prove
we can use the lemma to prove
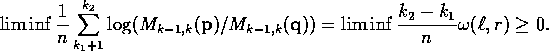
Theorem 3 follows.