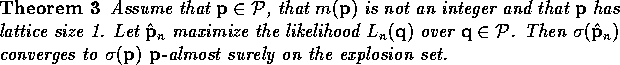
We are now in a position to use the theorem of the previous section to establish the following theorem.
If 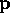 is concentrated on a single point then only one trajectory is
possible and
is concentrated on a single point then only one trajectory is
possible and
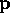 assigns probability 1 to this trajectory maximizing the
likelihood.
We assume that
assigns probability 1 to this trajectory maximizing the
likelihood.
We assume that 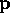 has lattice size 1; we have not pursued the
details for
other lattice sizes, though we believe the additional complications
are not serious.
We are also confident that the restriction that
has lattice size 1; we have not pursued the
details for
other lattice sizes, though we believe the additional complications
are not serious.
We are also confident that the restriction that 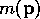 not be an
integer is
inessential but have not been able to prove it.
not be an
integer is
inessential but have not been able to prove it.
The theorem is proved in several steps. First we use the fact that
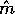 is the exact mle of
is the exact mle of 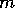 to prove that we can maximize over
distributions
to prove that we can maximize over
distributions
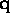 whose mean is not very different from that of
whose mean is not very different from that of 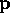 . When
the mean of
. When
the mean of 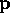 is not an integer all such
is not an integer all such 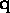 have variances bounded away from 0
and we can restrict
our attention to distributions in
have variances bounded away from 0
and we can restrict
our attention to distributions in 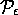 for some
positive
for some
positive  .
For such
.
For such 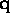 the likelihood can be approximated by a product of
two
terms. The first of these two terms arises from the normal
approximation to
the distribution of
the likelihood can be approximated by a product of
two
terms. The first of these two terms arises from the normal
approximation to
the distribution of 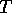 . This term can be maximized explicitly over
the class of
distributions
. This term can be maximized explicitly over
the class of
distributions 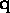 whose variance differs by more than
whose variance differs by more than  from that of
from that of 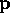 .
The maximum value will then be shown to be
smaller than the corresponding term in the approximation for the
likelihood under
.
The maximum value will then be shown to be
smaller than the corresponding term in the approximation for the
likelihood under
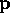 . The second of the two
terms arises from the distribution of the residue classes
. The second of the two
terms arises from the distribution of the residue classes 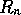 .
Under
.
Under 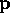 and any
other single
and any
other single 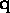 whose lattice size is 1 the sequence
whose lattice size is 1 the sequence 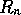 is
asymptotically iid
and uniform on the set of possible residue classes. For distributions
is
asymptotically iid
and uniform on the set of possible residue classes. For distributions
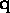 whose
lattice size is not 1 we can show that almost every (for
whose
lattice size is not 1 we can show that almost every (for 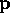 )
trajectory eventually
has an initial segment whose
)
trajectory eventually
has an initial segment whose 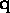 probability is 0. The problem
remaining is one of
uniformity. For any
probability is 0. The problem
remaining is one of
uniformity. For any  there will be
there will be 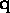 which have lattice size 1
but are very
close to a distribution whose lattice size is larger than 1. For such
which have lattice size 1
but are very
close to a distribution whose lattice size is larger than 1. For such
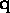 the
likelihood of the initial segment will not be exactly 0 but at the
same time the
sequence
the
likelihood of the initial segment will not be exactly 0 but at the
same time the
sequence 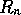 will not be approximately uniform under
will not be approximately uniform under 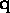 .
Most of the notational difficulty in what follows is dedicated to
dealing with such
.
Most of the notational difficulty in what follows is dedicated to
dealing with such
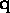 .
.
We will use the notation 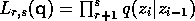 so that the
likelihood is
so that the
likelihood is 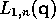 . Let
. Let 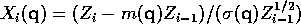 be
be 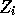 standardized for
standardized for 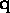 . In what
follows
. In what
follows
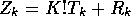 with
with 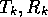 integers and
integers and 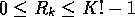 .
Throughout, lower case letters will be used to denote observed
values of such
random
variables as
.
Throughout, lower case letters will be used to denote observed
values of such
random
variables as 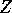 ,
, 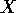 and so on. Our approximation to
and so on. Our approximation to 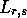 will
be
will
be
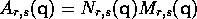 where
where
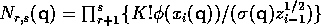 and
and
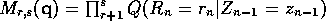 .
.
We will need the following facts about branching processes. References may be found in Guttorp(1991).
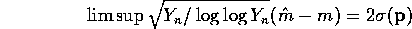
almost surely.
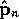 for which
for which
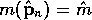 (Keiding and Lauritzen, 1978).
(Keiding and Lauritzen, 1978).
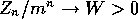 almost surely.
almost surely.
almost surely.