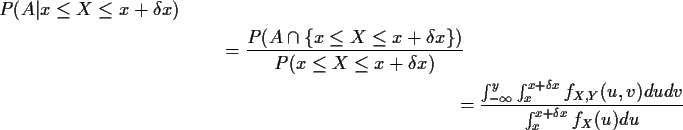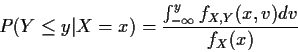Goals of Today's Lecture:
Events A and B independent if
Events Ai,
![]() are independent if
are independent if
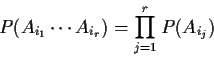
Example: p=3
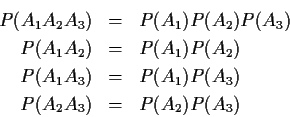
Example: Toss a coin twice. If A1 is the event that
the first toss is a Head, A2 is the event that the second toss
is a Head and A3 is the event that the first toss and the second
toss are different.
then
P(Ai) =1/2 for each i and for ![]()
Rvs
![]() are
independent if
are
independent if
![]() -fields
-fields
![]() are
independent if
are
independent if
Theorem:
1: If X and Y are independent then
2: If X and Y are independent and have joint density
fX,Y(x,y) then X and Y have densities, say fX and fY,
and for almost every pair (x,y)
3: If X, Y independent with marginal densities
fX and fY then (X,Y) has joint density
fX,Y(x,y) given by
4: If
5: If (X,Y) has density f(x,y) and there are functions
g(x) and h(y) such that
Proof:
1: By definition
![]() ,
,
![]() independent so
independent so
2:
Suppose
![]() ,
,
![]() ,
,
![]() Borel. Then
Borel. Then
![]() .
Hence
.
Hence
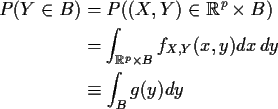
so Y has density g defined by
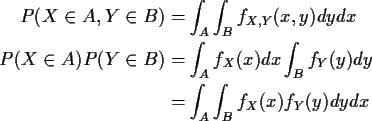
Since
![]() we see that for any sets
A and B
we see that for any sets
A and B
3: For any A and B Borel
![\begin{align*}P(X \in A, Y \in B) & = P(X\in A)P(Y \in B)
\\
&= \int_Af_X(x)dx \int_B f_Y(y) dy
\\
&= \int_A\int_B f_X(x)f_Y(y) ]dydx
\end{align*}](img33.gif)
Define
g(x,y) = fX(x)fY(y).
For
![]()
Monotone Class: collection ![]() of subsets of
a given set, closed under increasing
countable unions and decreasing countable intersections:
of subsets of
a given set, closed under increasing
countable unions and decreasing countable intersections:
Lemma: The smallest monotone class containing a field ![]() is
a
is
a ![]() -field.
-field.
Field: like ![]() -field but only
finite unions and intersections.
-field but only
finite unions and intersections.
Proof of Lemma: Let ![]() be
smallest monotone class containing
be
smallest monotone class containing
![]() (intersection of all monotone classes containing
(intersection of all monotone classes containing
![]() ).
Put
).
Put
![]() .
.
Now apply lemma to 3.
Rectangle: set
![]() where A, B Borel.
where A, B Borel.
A finite union of rectangles may be written as a finite disjoint union of rectangles so (1) holds for any such C.
The complement of a rectangle may be rewritten as a finite disjoint union of rectangles.
The collection ![]() of subsets of
of subsets of
![]() for which (1)
holds contains the field of all finite disjoin unions of
rectangles.
for which (1)
holds contains the field of all finite disjoin unions of
rectangles.
![]() is a monotone class by the dominated
convergence theorem.
is a monotone class by the dominated
convergence theorem.
Application of the dominated convergence theorem.
![]() has integral
equal to 1 by Tonelli's theorem. If
has integral
equal to 1 by Tonelli's theorem. If
![]() put
put
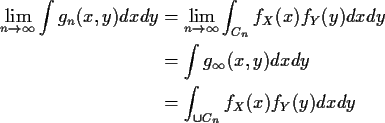
So ![]() contains smallest
contains smallest ![]() field containing this field.
field containing this field.
Every open rectangle is in this field so in ![]() .
.
Every open set is a countable union of open rectangles and so in ![]() .
.
Thus ![]() is a
is a ![]() field containing the open sets
and so must contain the Borel
field containing the open sets
and so must contain the Borel ![]() field.
field.
4: Monotone class argument: Homework 1.
5:
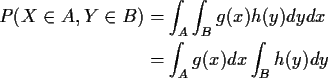
Take
![]() to see that
to see that
Def'n:
P(A|B) = P(AB)/P(B) if
![]() .
.
Def'n: For discrete rvs X, Y conditional
pmf of Y given X is
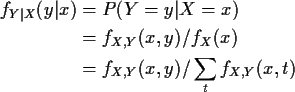
Problem for absolutely continuous X:
P(X=x) = 0 for all
x.
Solution is to take a limit