Postscript version of this page

STAT 870 Lecture 2

Goals of Today's Lecture:

• Discuss properties of Borel sets.

• Define random variables.

• Discuss Lebesgue measure, null sets.

Formal definitions:

The Borel $\sigma$-field in ${\Bbb R}^p$ is the smallest $\sigma$-field in ${\Bbb R}^p$ containing every open ball

$$B_y(r) = \{ x\in {\Bbb R}^p: \vert x-y\vert < r\}\, .$$

(To see that there is, in fact, such a ``smallest'' $\sigma$-field you prove the following assertions:

1.

The intersection of an arbitrary family of $\sigma$-fields is a $\sigma$-field. [Homework set 1.]

2.

There is at least one $\sigma$-field of subsets of ${\Bbb R}^p$ containing every open ball. [Homework set 1.]

Now define the Borel $\sigma$-field in ${\Bbb R}^p$ to be

$${\cal B}({\Bbb R}^p) = \cap {\cal F}$$

where the intersection runs over all $\sigma$-fields ${\cal F}$which contain every open ball.)

Every common set is a Borel set, that is, in the Borel $\sigma$-field. For instance, let O be an open set. Then I will prove that O is Borel. For each x in O there is a point y all of whose co-ordinates are rational numbers and a rational number r such that

$$x \in B_y(r) \subset O$$

Now O is the union of all these B_y(r). (Every $x\in O$ is in one of the B_y(r) and every point in any B_y(r) is in O.) But the union is countable because there are only countably many possible pairs (y,r)with all the co-ordinates rational numbers. [Homework set 1.]

Random Variables

An ${\Bbb R}^p$ valued random variable is a map $X:\Omega\mapsto {\Bbb R}^p$ such that when A is Borel then $\{\omega\in\Omega:X(\omega)\in A\} \in \cal F$.

Fact: this is equivalent to

$$\left\{ \omega\in\Omega: X_1(\omega) \le x_1, \ldots , X_p (\omega) \le x_p \right\} \in \cal F$$

for all $(x_1,\ldots,x_p)\in {\Bbb R}^p$. [Homework set 1.]

Jargon and notation: we write $P(X\in A)$ for $P(\{\omega\in\Omega:X(\omega)\in A\})$ and define the distribution of X to be the map

$$A\mapsto P(X\in A)$$

which is a probability on the set ${\Bbb R}^p$ with the Borel $\sigma$-field rather than the original $\Omega$ and ${\cal F}$.

Cumulative Distribution Function (or CDF) of X is the function F_X on ${\Bbb R}^p$ defined by

$$F_X(x_1,\ldots, x_p) = P(X_1 \le x_1, \ldots , X_p \le x_p)$$

Properties of F_X:

1.

$0 \le F(x) \le 1$.

2.

$x> y \Rightarrow F(x) \ge F(y)$ (monotone non-decreasing).

3.

$\lim_{x\to - \infty} F(x) = 0$

4.

$\lim_{x\to \infty} F(x) = 1$

5.

$\lim_{x\searrow y} F(x) = F(y)$ (right continuous).

6.

$\lim_{x\nearrow y} F(x) \equiv F(y-)$ exists.

7.

F(x)-F(x-) = P(X=x).

8.

F_X(t) = F_Y(t) for all t implies X and Y have same distribution: $P(X\in A) = P(Y\in A)$ for any Borel A.

Distribution of rv X is discrete (or just X is discrete) if there is a countable set $x_1,x_2,\cdots$ such that

$$P(X \in \{ x_1,x_2 \cdots\}) =1 = \sum_i P(X=x_i) \, .$$

Discrete density or probability mass function of X is

$$f_X(x) = P(X=x) \, .$$

Distribution of rv X is absolutely continuous if there is a function f such that

$$P(X\in A) = \int_A f(x) dx$$

for any Borel A; p dimensional integral.

Condition equivalent when p=1to

$$F(x) = \int_{-\infty}^x f(y) \, dy$$

or for general p to
$$\begin{multline*}F(x_1,\ldots,x_p) \\ = \int_{-\infty}^{x_1} \cdots \int_{-\infty}^{x_p} f(y_1,\ldots,y_p)dy_1\cdots dy_p \, . \end{multline*}$$

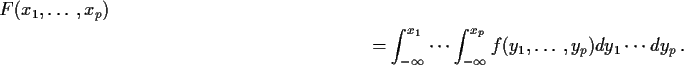
We call f the density of X. For most values of x we then have F is differentiable at x and, for p=1

$$F^\prime(x) =f(x)$$

or in general

$$\frac{\partial^p}{\partial x_1 \cdots \partial x_p} F(x_1,\ldots,x_p)=f(x_1,\ldots,x_p) \, .$$

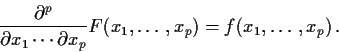
Uniqueness? No. But if f and g densities of X then the Lebesgue measure (wait for it) of

$$\{x: f(x) \neq g(x)\}$$

is 0.

Measurability

1.

$f: {\Bbb R}^p \mapsto {\Bbb R}^q$ is Borel if $\forall$ Borel set $B\subset {\Bbb R}^q$ the inverse image

$$f^{-1}(B) = \{x\in {\Bbb R}^p: f(x) \in B\}$$

is a Borel set.

2.

If $f: {\Bbb R}^p \mapsto {\Bbb R}^q$ and $g: {\Bbb R}^q \mapsto {\Bbb R}^r$ are Borel then so is $h=g\circ f$, (composition of g and f) from ${\Bbb R}^p$ to ${\Bbb R}^r$.

3.

Every continuous function is Borel.

4.

f is Borel if and only if f^-1(O) is Borel for each open set O. Similarly for closed.

5.

If f_n is a sequence of Borel functions then

$$g \equiv \limsup f_n$$

is Borel. Same for $\liminf f_n$ and others.

6.

X an ${\Bbb R}^p$ valued rv, $f: {\Bbb R}^p \mapsto {\Bbb R}^q$ Borel then Y=f(X) is ${\Bbb R}^q$ valued rv.

Lebesgue Measure

There is a probability measure $\lambda$ defined on the Borel subsets of [0,1] which agrees with length for intervals: $\lambda([a,b]) = b-a$for $0 \le a \le b \le 1$.

Extend $\lambda$ to arbitrary Borel subsets of ${\Bbb R}$; p dimensional generalization of volume also possible.

Extension has properties of probability measure except $\lambda({\Bbb R}) = \infty$not 1. Such an object is a measure.

The measure $\lambda$ is translation invariant:

$$\lambda(c+B) = \lambda(B)$$

for any Borel set B, real number c:

$$c+B = \{y: y=c+x \text{ for some } x\in B\} \, .$$

Borel set B is Lebesgue null if $\lambda(B)=0$:

1.

The rational numbers ${\Bbb Q}$.

2.

The Cantor set (all real numbers x in [0,1] whose expansions in base 3 may be written without the digit 1).

If $A \subset B$ and B is a Lebesgue null Borel set then it is natural to define $\lambda(A)=0$ even if A is not Borel. We call all such A Lebesgue null sets. A set $A \subset {\Bbb R}$is Lebesgue measurable if we can write $A=B \cup N$ with B Borel and N a Lebesgue null set. The family of all Lebesgue measurable sets is a $\sigma$-field (which is much larger than the Borel $\sigma$-field).

A property of a function f(x) which holds except for a set N of x which is a Lebesgue null set is said to hold almost everywhere.