Vancouver, June 4-6 2009

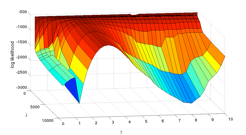
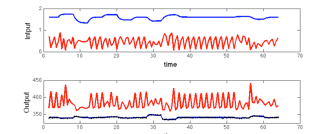
Dynamic models, usually written in forms of differential equations (DEs), describe the rate of change of a process. They are widely used in medicine, engineering, ecology and a host of other applications. One central and difficult problem is how to estimate DE parameters from noisy data. Ramsay et al. (2007) proposed the generalized profiling method to solve this problem. DE solutions are approximated by nonparametric functions, which are estimated by penalized smoothing with DE-defined penalty. The computation is much faster than other methods. A modified delta method is proposed to estimate variances of DE parameters, which include all the uncertainty of the smoothing process. We have extended the generalized profiling method to estimate time-varying parameters. A roughness penalty term is included to control the smoothness of the time-varying parameters. Simulations show that this method provides better estimates than the two-stage estimation strategy.

This is joint work with Jianhua Huang, Texas A&M University

Jiguo Cao

Assistant Professor

Department of Statistics and

Actuarial Science

Simon Fraser University

Burnaby, British Columbia