Vancouver, June 4-6 2009

Probability can be viewed as a multi-valued logic for plausible reasoning that extends Boolean propositional logic to the case of incomplete information. The key idea is that the probability P[b|c] of a statement (or proposition) b given the information in statement c is a measure of how plausible b is based on c. Boolean logic deals with the special case of complete information where the truth or falsity of b is known from c, that is, P[b|c]=1 or P[b|c]=0, respectively. The physicist R.T. Cox was the first to derive the probability logic axioms from those of Boolean logic by using them to put constraints on the functional dependence of the probabilities of conjunction, disjunction and negation of statements on more elementary probabilities. Kolmogorov`s axioms for a probability measure, which are neutral with respect to the interpretation of probability, are a special case where the statements describe membership in sets. This interpretation of probability is consistent with the Bayesian point of view that probability represents a degree of belief in a statement but probability logic puts more emphasis on the incompleteness of the conditioning information and on information-theoretic ideas due to C. Shannon and E.T. Jaynes. Probability logic provides a rigorous unifying framework for treating modeling uncertainty, along with input uncertainty, when using models to predict the response of a real system. It gives a meaning for the concept of "the probability of a model" as a measure of the relative plausibility of the model within a proposed set of models.

In the presentation I will give an overview of the foundations of probability logic and its application to quantifying uncertainty for predictive modeling of dynamic systems, which is based on a graduate class on these topics that I teach at Caltech. By a system I mean any part of the world, natural or man-made, that we wish to conceptually isolate for study, where its interactions with the rest of the world are modeled through its inputs and

outputs. A key concept is a stochastic system (or Bayesian) model class, which consists of a chosen set of probabilistic input-output predictive models for a system together with a chosen probability distribution, the prior, over this set that quantifies the initial relative plausibility of each predictive model in the set. These probability models are viewed as

representing a state of knowledge about the system conditional on the available information and not as inherent properties of the system. They quantify uncertainty when there is missing information, allowing the fruitful application of the probability axioms without invoking the vague and unprovable belief of `inherent randomness` (or `aleatory uncertainty`) which does not provide an operational meaning for the probability of a model. All probabilities are conditional on the chosen fundamental probability models for the model class, and possibly other specified information (e.g. system data). A model class may be constructed through stochastic embedding of a parameterized deterministic model where Jaynes` Principle of Maximum Information Entropy is used to develop a

probability model for the prediction error.

Based purely on deductions from the probability axioms, a model class leads to both prior and posterior robust predictive analysis. These analyses are robust to modeling uncertainty because they automatically treat the sensitivity of the predictive models to their parameter values by including the predictions of all possible models in the model class, weighted by their prior or posterior probabilities. They not only treat `parametric uncertainty` (i.e. uncertainty about which model in a proposed set should be used to represent the input-output behavior of the system) but also `non-parametric uncertainty` (or `unmodeled dynamics`) due to the existence of prediction error between any deterministic model output and the real system output. Prior robust analyses are of importance when designing a system whereas posterior robust analyses can be used to

improve predictive modeling of operating systems. Since there is always uncertainty in choosing a model class to represent a system, one can also choose a set of candidate model classes. The probability axioms then lead naturally to prior and posterior hyper- robust predictive models that combine the predictions of all model classes in the set. In the latter case, the posterior probability of each model class from Bayes` Theorem controls its probabilistic contribution to the hyper-robust predictions and if this is negligible, the model class may be dropped from the set of candidates; this provides a rigorous method for model class selection. A new information-theoretic result shows that the posterior probability incorporates a trade-off between the average data-fit of a model class and a measure of its complexity, specifically, the relative entropy (Kullback-Leibler information) of the posterior to the prior which is a measure of the information gain from the data by the model class.

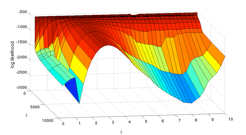
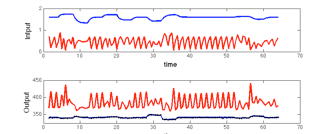
The challenge in implementing robust predictive analyses is that integrals over high- dimensional parameter spaces are usually involved that cannot be evaluated analytically, nor numerically in a straight-forward way. Some useful computational tools that we have used are Laplace`s method of asymptotic approximation and Markov Chain Monte Carlo methods, including multi-level Metropolis-Hastings algorithms with tempering, the Gibbs sampler and the Hybrid Monte Carlo algorithm. Particle filter algorithms are useful for sequential Bayesian state estimation when the Kalman filter is not applicable because of non-linear dynamics and/or non-Gaussian probability models. Some illustrative results will be presented involving the application of these algorithms to dynamic systems that

come from past work by my research group.

James Beck

Professor of Engineering and Applied Science
Department of Civil Engineering and Applied Mechanics

California Institute of Technology

Pasadena, California