Compute and plot the autocovariance function of X.
Solution:
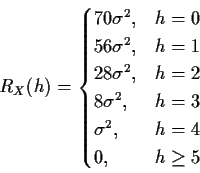
Solution: I should have simply asked the question with ``suppose
that
![]() are iid with mean 0 and variance
are iid with mean 0 and variance ![]() " instead
of the first sentence.
We have
" instead
of the first sentence.
We have
![]() The autocovariance function of X is
The autocovariance function of X is
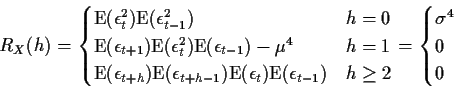
Thus Xt is second order white noise. In fact, from question 4 this sequence is strongly stationary. It is also second order white noise but it is not strict sense white noise.
where
Solution: This is my rephrasing of the question. To compute the
autocovariance function you have two possibilities. First you can factor
with the
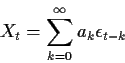
where
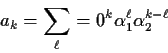
The autocovariance function is then
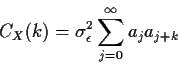
This would be rather tedious to compute; you would have to decide how many terms to take in the infinite sums.
The second possibility is the recursive method:
To get started you need values for CX(0) and CX(1). The simplest thing to do, since the value of
so that
You can use this for
Now the roots
![]() are of the form
are of the form
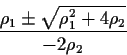
The stationarity conditions are that both of these roots must be larger than 1 in modulus.
If
![]() then the two roots are real. Set them
equal to 1 and then to -1 to get the boundary of the region of interest:
then the two roots are real. Set them
equal to 1 and then to -1 to get the boundary of the region of interest:
gives
It is now not hard to check that the inequalities
and
guarantee, for
When the discriminant
![]() is negative the two
roots are complex conjugates
is negative the two
roots are complex conjugates
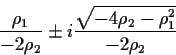
and have modulus squared
which will be more than 1 provided
Finally for ![]() the process is simply an AR(1) which will
be stationary for
the process is simply an AR(1) which will
be stationary for
![]() .
Putting together all these limits
gives a triangle in the
.
Putting together all these limits
gives a triangle in the
![]() plane bounded by the lines
plane bounded by the lines
![]() ,
,
![]() and
and ![]() .
.
is strictly stationary. What property must g have to guarantee the analogous result with strictly stationary replaced by
Solution: You must prove the following assertion: for any k and
any
![]() we have
we have
(for the mathematically inclined you need this for ``Borel sets A".) Define g* by
so that
and
Then
where
is the inverse image of A under the map g*. In fact the probability on the right is the definition of the probability on the left!
(REMARK: A number of students worried about whether or not you could take
this
(g*)-1(A); I suspect there were worried about the existence of
a so-called functional inverse of g*. The latter exists only if g*is a bijection: one-to-one and onto. But the inverse image B of Aexists for any g*; it is defined as
![]() .
As a simple
example if
g*(x) = x2 then there is no functional inverse of g* but
for instance,
.
As a simple
example if
g*(x) = x2 then there is no functional inverse of g* but
for instance,
so that the inverse image of [1,4] is perfectly well defined.)
For the special case t=0 we also get
But since X is stationary
from which we get the desired result.
For the second part, if g is affine, that is
![]() for some
for some ![]() vector A and a constant b then Y will have
stationary mean and covariance if X does. In fact I think the condition
is necessary but do not know a complete proof.
vector A and a constant b then Y will have
stationary mean and covariance if X does. In fact I think the condition
is necessary but do not know a complete proof.
- (a)
- Derive the autocovariance of the process X.
Solution:
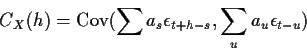
simplifies to
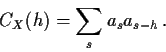
- (b)
- Show that
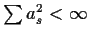 implies
implies
![\begin{displaymath}\lim_{N\to\infty} E[(X_t - \sum_{-N}^N a_s \epsilon_{t-s})^2] = 0
\end{displaymath}](img66.gif)
This condition shows that the infinite sum defining X converges ``in the sense of mean square''. It is possible to prove that this means that X can be defined properly. [Note: I don't expect much rigour in this calculation.Solution: I had in mind the simple calculation
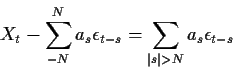
which has mean 0 and variance
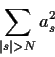
The latter quantity converges to 0 since
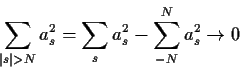
More rigour requires the following ideas. I had no intention for students to discover or use these ideas but some, at least, were interested to know.
Let L2 be the set of all random variables X such that
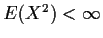 where we agree to regard two random variables X1 and
X2 as being the same if
E((X1-X2)2)=0.
(Literally we define them to be equivalent in this case and then let
L2 be the set of equivalence classes.) It is a mathematical fact about
L2 that it is a Banach space, or a complete normed vector space with a
norm defined by
where we agree to regard two random variables X1 and
X2 as being the same if
E((X1-X2)2)=0.
(Literally we define them to be equivalent in this case and then let
L2 be the set of equivalence classes.) It is a mathematical fact about
L2 that it is a Banach space, or a complete normed vector space with a
norm defined by
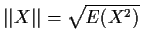 .
The important point is that any
Cauchy sequence in L2 converges to some limit.
.
The important point is that any
Cauchy sequence in L2 converges to some limit.
Define
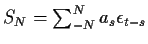 and note that
for
N1 < N2 we have
and note that
for
N1 < N2 we have
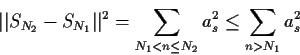
which shows that SN is Cauchy because the sum converges. Thus there is an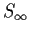 such that
such that
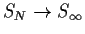 in L2which means
in L2which means
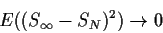
This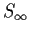 is precisely our definition of Xt.
is precisely our definition of Xt.
and for the minimizing A evaluate the mean squared error in terms of the autocorrelation and the variance of Xt.
Solution: I added the mean 0 later because you need it and I
had forgotten it. You get
![\begin{eqnarray*}E[(X_{t+d}-AX_t)^2] & = & E(X_{t+d}^2) -2AE(X_{t+d}X_t) + A^2 E(X_t^2) \cr
& = & C_X(0) -2A C_X(d) +A^2 C_X(0)
\end{eqnarray*}](img79.gif)
this quadratic is minimized when its derivative -2CX(d)+2ACX(0) is 0 which is when
Put in this value for A to get a mean squared error of
or just
Solution: The stationarity comes from question 4. To compute the
mean and covariance of Y we use the fact that the moment generating
function of a
![]() random variable is
random variable is
![]() .
Since E(Yt) is just the mgf of Xt at s=1we see that the mean of Y is just
.
Since E(Yt) is just the mgf of Xt at s=1we see that the mean of Y is just
![]() .
To compute
the covariance we need
.
To compute
the covariance we need
which is just the mgf of Xt+Xt+h at 1. Since Xt+Xt+h is
or
(Without the 1/2 it's called the variogram.) Evaluate
Solution:
![\begin{eqnarray*}\gamma_X(m) & = & \frac{1}{2} E[(X_{t+m}-X_t)^2] \cr
& = & \fr...
...} (C_X(0) +C_X(0) -2 C_X(m)) \cr
& = & C_X(0)(1-\rho_X(m)) \, .
\end{eqnarray*}](img94.gif)