Definition: Two processes X and Y are jointly (strictly) stationary
if
Definition: If X is stationary then we call
![]() the autocovariance function of X.
the autocovariance function of X.
Definition: If X and Y are jointly stationary then we call
![]() the cross-covariance
function.
the cross-covariance
function.
Notice that CX(-h) = CX(h) and CXY(h) = CYX(-h) for all h and similarly for correlation
Definition: The autocorrelation function of X is
Fact: If X and Y are jointly stationary then aX+bY is stationary for any constants a and b.
The goal of this section is to develop tools to permit us to choose a model for a given series X. We will be attempting to fit an ARMA(p,q) and our first step is to learn how to choose p and q. We will try to get small values of these orders and our efforts are focused on the cases with either p or q equal to 0. We use the autocorrelation or autocovariance function to do model identification.
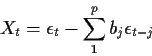
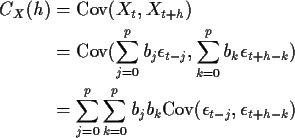
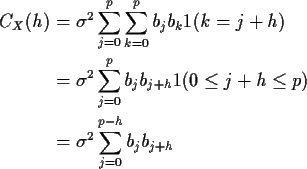
Notice that if h>p (or h < -p) then we get CX(h) =0.
Jargon: We call h the lag and say that for an MA(p) process the autocovariance function is 0 at lags larger than p.
To identify an MA(p) look at a graph of an
estimate
![]() and look for a lag where it suddenly
decreases to (nearly) 0.
and look for a lag where it suddenly
decreases to (nearly) 0.
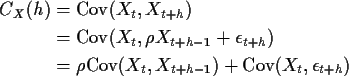
For h>0 the term
![]() .
This gives
.
This gives
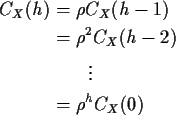
This gives
Notice that RX(h) decreases geometrically to 0 but is never actually 0.
Remark: If ![]() is small so that
is small so that ![]() is
very small then an AR(1) process is approximately the same
as an MA(1) process: we nearly have
is
very small then an AR(1) process is approximately the same
as an MA(1) process: we nearly have
![]() .
.