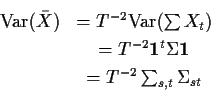Postscript version of these notes
STAT 804: Lecture 1
I begin the course by presenting plots of some time series and
then present some discussion of the series using some of the jargon
we will study. Then I will introduce some basic technical ideas.
Plots of some series
Comments on the data sets:
- Top left: Sunspot data. Each month the average number of
sunspots is recorded. Notice the apparent periodicity, the large
variability when the series is at a high level and the small variability
when the series is at a small level. This series is likely to be quite
stationary over the time span we have been able to observe it, though it
may have a nearly perfectly periodic component.
- Top right: Annual sales of lynx pelts to the Hudson's Bay Company.
There is a clear cycle of about 10 years in length. Might there be a longer
term cycle? Is the cycle produced by a strictly periodic phenomenon or
by a dynamic system close to a periodic system?
- Middle left: Mean monthly flow rates for the Fraser River at Hope.
There are signs of lower variability at low levels suggesting
transformation. There is a clear annual cycle which will have to be removed
to look for stationary residuals.
- Middle right: Monthly unemployment numbers in Canada. Notice the
probably presence of a slow upward trend; such a trend should be
present in the presence of a growing population.
This series is not stationary. The trend is not too linear with
some apparent long term cycles perhaps which produce an S shaped curve.
- Lower left: Carbon Dioxide above Mauna Loa (a Hawaian volcano).
There is a clear trend and an annual cycle but you might well hope
that after compensating for these the remainder would be stationary.
- Lower right: Changes in the length of the Earth's day. This sort of
very smooth graph with long runs going up and down suggests integration.
We will look at differencing as a method of producing a series with less
long range dependence.
I made these plots with S-Plus using the following code:
postscript("tsplots.ps",horizontal=F)
par(mfrow=c(3,2))
tsplot(sunspots,main="Mean Monthly Sunspot Numbers")
tsplot(lynx, main="Annual Sales of Lynx\n to Hudson's Bay Co.")
tsplot(flow, ylab="Cubic Meters per Second",
main="Mean Monthly Flow\nFraser River at Hope")
tsplot(unemployment, main="Unemployment: Canada",ylab="Thousands")
tsplot(co2, main="CO2 concentration: Mauna Loa",
ylab="Parts per Million")
tsplot(changes, main="Changes in length of day", ylab="Seconds?")
dev.off()
Basic jargon
We will study data of the sort plotted here using the
idea of a stochastic process. Technically, a
stochastic process is a family
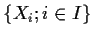 of random variables indexed by a set I. In practice the
jargon is used only when the Xi are not independent.
of random variables indexed by a set I. In practice the
jargon is used only when the Xi are not independent.
If 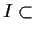 Real Line, then we often call
Real Line, then we often call
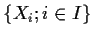 a time series. Of course the usual situation is that i actually
indexes a time point at which some measurement was made.
a time series. Of course the usual situation is that i actually
indexes a time point at which some measurement was made.
Two important special cases are I an interval in R, the real
line, in which case we say X is a series in continuous time,
and where
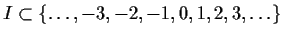 in which case X is in discrete time.
in which case X is in discrete time.
Here is a list of some models used for time series:
- Stochastic Process Models (note the conflict of jargon).
- Population models
- Birth and Death Processes -- which describe the size of a
population in terms of random births and deaths.
- Markov chain models -- where the future depends on the present
and not, in addition, on the past. Birth and Death processes are
special cases.
- Galton-Watson-Bienaymé processes -- a Markov chain model
for the size of generations of a populations. The model specifies that
the size of the nth generation is the sum of the family sizes of each
individual in the n-1st generation and that these family sizes
have an iid distribution. Many generalizations are in use.
- Branching processes -- are a continuous time version of
the Galton-Watson-Bienaymé process.
- Diffusion models
- Brownian Motion
- Random Walk
- Stochastic Differential Equations -- models like
where B is a Brownian motion.
- Linear Time Series Models -- linear filters applied to white noise.
This course is about the discrete time version of these linear time
series models. We will assume throughout that we have data
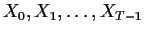 where the Xt are real random variables.
where the Xt are real random variables.
A model is a family
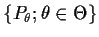 of possible
joint distributions for
of possible
joint distributions for
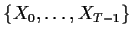 .
.
Goal: guess the true value of 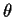 .
(Notice that it is an assumption
that the distribution of the data is, in fact one of the possibilities.)
.
(Notice that it is an assumption
that the distribution of the data is, in fact one of the possibilities.)
The question is this: is it possible to guess the true value of 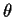 ?
Will collecting more data (increasing T) make more accurate estimation
of
?
Will collecting more data (increasing T) make more accurate estimation
of 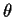 possible? The answer is no, in general. For instance in the
Galton Watson process even when you watch infinitely many generations you
don't get enough data to nail down the parameter values.
possible? The answer is no, in general. For instance in the
Galton Watson process even when you watch infinitely many generations you
don't get enough data to nail down the parameter values.
Example: Suppose that
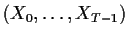 has a
multivariate normal distribution with mean vector
has a
multivariate normal distribution with mean vector
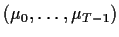 and
and 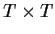 variance covariance matrix
variance covariance matrix 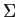 .
The big problem is that with T data points you have
T+T(T-1)/2parameters to estimate; this is not possible. To make progress
you must put restrictions on the parameters
.
The big problem is that with T data points you have
T+T(T-1)/2parameters to estimate; this is not possible. To make progress
you must put restrictions on the parameters 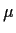 and
and 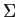 .
For instance you might assume one of the following:
.
For instance you might assume one of the following:
- 1.
- Constant mean:
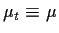 .
.
- 2.
- Linear trend;
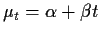 .
.
- 3.
- Linear trend and sinusoidal variation:
We can estimate the p here by regression but we still have a problem -
we can't get standard errors. For instance, we might estimate
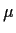 in 1) above using
in 1) above using 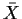 .
In that case
.
In that case
where 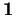 is a column vector of T 1s. SO: we must model
is a column vector of T 1s. SO: we must model
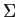 as well as
as well as 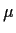 .
.
The assumption we will make in this course is of stationarity:
If so then for all t and h we find
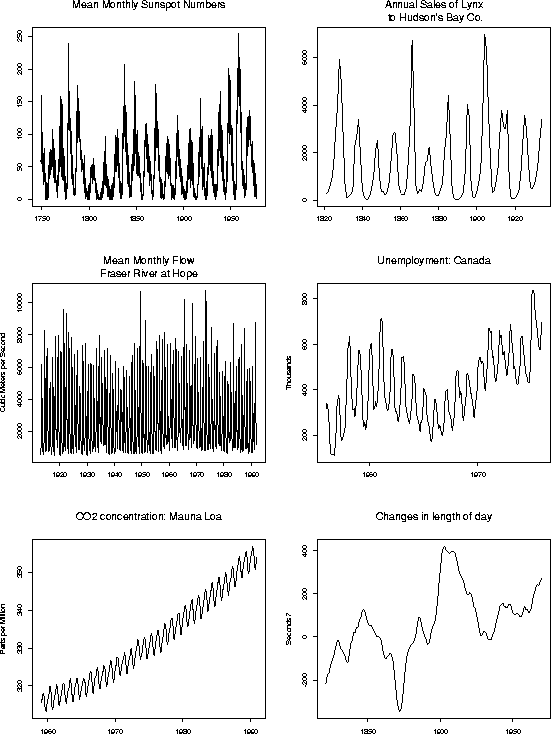
(which we will call the autocovariance function of X). Then
we see the a 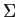 has C(0) down the diagonal, C(1) down the
first sub and super diagonals, C(2) down the next sub and super
diagonals and so on. Such a matrix is called a Toeplitz matrix.
has C(0) down the diagonal, C(1) down the
first sub and super diagonals, C(2) down the next sub and super
diagonals and so on. Such a matrix is called a Toeplitz matrix.


Richard Lockhart
1999-09-19
![]() of random variables indexed by a set I. In practice the
jargon is used only when the Xi are not independent.
of random variables indexed by a set I. In practice the
jargon is used only when the Xi are not independent.
![]() Real Line, then we often call
Real Line, then we often call
![]() a time series. Of course the usual situation is that i actually
indexes a time point at which some measurement was made.
a time series. Of course the usual situation is that i actually
indexes a time point at which some measurement was made.
![]() in which case X is in discrete time.
in which case X is in discrete time.
![]() where the Xt are real random variables.
where the Xt are real random variables.
![]() of possible
joint distributions for
of possible
joint distributions for
![]() .
.
![]() .
(Notice that it is an assumption
that the distribution of the data is, in fact one of the possibilities.)
.
(Notice that it is an assumption
that the distribution of the data is, in fact one of the possibilities.)
![]() ?
Will collecting more data (increasing T) make more accurate estimation
of
?
Will collecting more data (increasing T) make more accurate estimation
of ![]() possible? The answer is no, in general. For instance in the
Galton Watson process even when you watch infinitely many generations you
don't get enough data to nail down the parameter values.
possible? The answer is no, in general. For instance in the
Galton Watson process even when you watch infinitely many generations you
don't get enough data to nail down the parameter values.
![]() has a
multivariate normal distribution with mean vector
has a
multivariate normal distribution with mean vector
![]() and
and ![]() variance covariance matrix
variance covariance matrix ![]() .
The big problem is that with T data points you have
T+T(T-1)/2parameters to estimate; this is not possible. To make progress
you must put restrictions on the parameters
.
The big problem is that with T data points you have
T+T(T-1)/2parameters to estimate; this is not possible. To make progress
you must put restrictions on the parameters ![]() and
and ![]() .
For instance you might assume one of the following:
.
For instance you might assume one of the following:
![]() in 1) above using
in 1) above using ![]() .
In that case
.
In that case