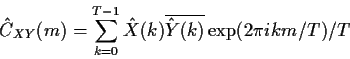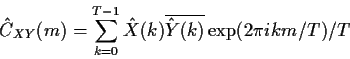STAT 804: 99-3
Assignment 5
- 1.
- Suppose X and Y are stationary independent processes with respective
spectra fX and fY. Compute the spectrum of Z=aX+Y.
- 2.
- Suppose X and Y are jointly stationary processes and we observe
them at times
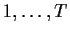 .
Define the
sample cross covariance
.
Define the
sample cross covariance
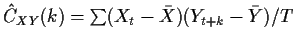 where are terms with index larger than T are interpreted as 0.
Show that the sample cross covariance can be computed from the discrete
Fourier transforms via
where are terms with index larger than T are interpreted as 0.
Show that the sample cross covariance can be computed from the discrete
Fourier transforms via
(or figure out the correct formula).
- 3.
- Derive the frequency response function for the recursive filter
Yt = a Yt-1 + Xt
and plot the modulus squared and argument of
the result for a = 0.8 and a=0.1.
- 4.
- Compute and plot estimates of the spectrum for the time series
fake for varying degrees of smoothing and compare the result to
the spectrum of your fitted ARIMA model.
- 5.
- Let
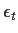 be a Gaussian white noise process. Define
be a Gaussian white noise process. Define
Compute and plot the spectrum of X.
- 6.
- For the filters A:
yt=xt-xt-12, B:
yt=xt-xt-1and C defined by applying A then B determine the power transfer functions,
plot them and interpret their effect on a spectrum. What is the effect of
these filters on seasonal series? (Consider what the spectrum of a series
with a strong seasonal effect is like.)
DUE: Monday, 6 December.
Richard Lockhart
1999-11-29