Postscript version of this assignment
STAT 804: 99-3
Assignment 2
- 1.
- Consider the ARIMA(1,0,1) process
Show that the autocorrelation function is
and
Plot the autocorrelation functions for the ARMA(1,1) process above, the AR(1)
process with
and the MA(1) process
on the same plot when
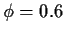 and
and
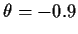 .
Compute and plot the partial autocorrelation functions up to lag 30. Comment
on the usefulness
of these plots in distinguishing the three models.
Explain what goes wrong when
.
Compute and plot the partial autocorrelation functions up to lag 30. Comment
on the usefulness
of these plots in distinguishing the three models.
Explain what goes wrong when 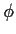 is close to
is close to 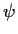 .
.
- 2.
- Suppose
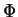 is a Uniform
is a Uniform![$[0,2\pi ]$](img11.gif) random variable. Define
random variable. Define
Show that X is weakly stationary. (In fact it is strongly stationary so
show that if you can.) Compute the autocorrelation function of X.
- 3.
- Show that X of the previous question satisfies the AR(2) model
for some value of 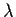 .
Show that the roots of the characteristic
polynomial lie on the boundary of the unit circle in the complex plain. (Hint:
show that
.
Show that the roots of the characteristic
polynomial lie on the boundary of the unit circle in the complex plain. (Hint:
show that
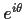 is a root if
is a root if 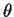 is chosen correctly.
Do not spend too much time on this question; the point is to
illustrate that AR(2) models can be found
whose behaviour is much like a sinusoid.)
is chosen correctly.
Do not spend too much time on this question; the point is to
illustrate that AR(2) models can be found
whose behaviour is much like a sinusoid.)
- 4.
- Suppose that Xt is an ARMA(1,1) process
- (a)
- Suppose we mistakenly fit an AR(1) model (mean 0) to Xusing the Yule-Walker estimate
In terms of 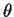 ,
,
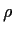 and
and 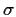 what is
what is 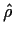 close to?
close to?
- (b)
- If we use this AR(1) estimate
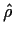 and calculate
residuals using
and calculate
residuals using
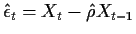 what kind of
time series is
what kind of
time series is
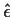 ? What will plots of the Autocorrelation and
Partial Autocorrelation functions of this residual series look like?
? What will plots of the Autocorrelation and
Partial Autocorrelation functions of this residual series look like?
Richard Lockhart
1999-10-12
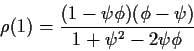
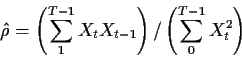
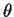 ,
,
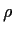 and
and 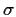 what is
what is 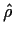 close to?
close to?
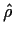 and calculate
residuals using
and calculate
residuals using
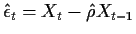 what kind of
time series is
what kind of
time series is
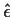 ? What will plots of the Autocorrelation and
Partial Autocorrelation functions of this residual series look like?
? What will plots of the Autocorrelation and
Partial Autocorrelation functions of this residual series look like?