Compute and plot the autocovariance function of X.
- (a)
- If g is some
function from Rp+1 to R show that
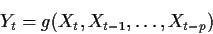
is strictly stationary. - (b)
- What property must g have to guarantee the
analogous result with strictly stationary replaced by
 order
stationary? [Note: I expect a sufficient condition on g; you need not
try to prove the condition is necessary.]
order
stationary? [Note: I expect a sufficient condition on g; you need not
try to prove the condition is necessary.]
where
- (a)
- Derive the autocovariance of the process X.
- (b)
- Show that
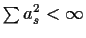 implies
implies
![\begin{displaymath}\lim_{N\to\infty} E[(X_t - \sum_{-N}^N a_s \epsilon_{t-s})^2] = 0
\end{displaymath}](img18.gif)
This condition shows that the infinite sum defining X converges ``in the sense of mean square''. It is possible to prove that this means that X can be defined properly. [Note: I don't expect much rigour in this calculation. Mathematically, you can't just define Xt as this question supposes since the sum is infinite. A rigourous treatment asks you to prove that the condition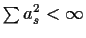 implies that
the sequence
implies that
the sequence
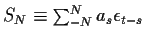 is a Cauchy
sequence in L2. Then you have to know that this implies the existence of a limit
in L2 (technically, the point is that L2 is a Banach space). Then you have to
prove that the calculation you made in the first part of the question is mathematically
justified.]
is a Cauchy
sequence in L2. Then you have to know that this implies the existence of a limit
in L2 (technically, the point is that L2 is a Banach space). Then you have to
prove that the calculation you made in the first part of the question is mathematically
justified.]
E[(Xt+d-AXt)2]
and for the minimizing A evaluate the mean squared error in terms of the autocorrelation and the variance of Xt.
(Without the 1/2 it's called the variogram.) Evaluate