Reading for Today's Lecture:
Goals of Today's Lecture:
Today's notes
Last time derived the Fourier inversion formula
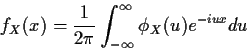
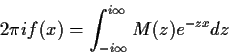
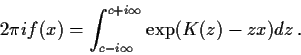
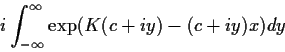
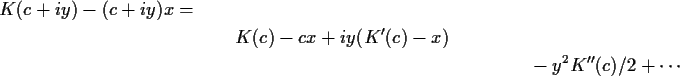

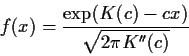
Essentially the same idea lies at the heart of the proof of
Sterling's approximation to the factorial function:
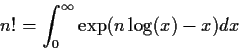
![\begin{displaymath}n! \approx \int_0^\infty \exp[n\log(n) - n -
(x-n)^2/(2n)] dx
\end{displaymath}](img17.gif)
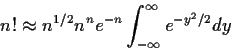
This tactic is called Laplace's method. Note that I am being very sloppy about the limits of integration; to do the thing properly you have to prove that the integral over x not near n is negligible.
1): Numerical calculations
Example: Many statistics have a distribution which is approximately that
of
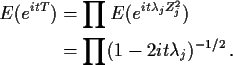
Here is how it works:
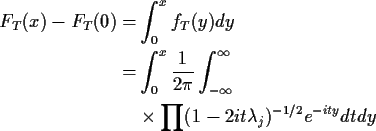
Multiply
![\begin{displaymath}\phi(t) = \left[\frac{1}{\prod(1-2it\lambda_j)}\right]^{1/2}
\end{displaymath}](img24.gif)
![\begin{displaymath}\phi(t) =
\left[\frac{\prod(1+2it\lambda_j)}{\prod(1+4t^2\lambda_j^2)}\right]^{1/2}
\end{displaymath}](img25.gif)
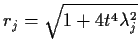 and
and
![\begin{displaymath}\phi(t) = \left[\frac{\prod r_j e^{i\sum\theta_j}}{\prod
r_j^2}\right]^{1/2}
\end{displaymath}](img30.gif)
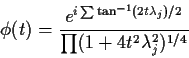
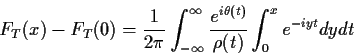
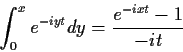
2): The central limit theorem (the version which is called ``local'') can be deduced from
the Fourier inversion formula:
if
![]() are iid with mean 0 and variance 1 and
are iid with mean 0 and variance 1 and
![]() then with
then with ![]() denoting the characteristic function of
a single X we have
denoting the characteristic function of
a single X we have
![\begin{align*}E(e^{itT}) = & E(e^{in^{-1/2} t\sum X_j})
\\
= & \left[\phi(n^{-...
...\
&
\left.+ n^{-1}t^2\phi^{\prime\prime}(0)/2 + o(n^{-1})\right]^n
\end{align*}](img39.gif)
But now
![]() and
and
![\begin{align*}E(e^{itT}) & \approx [1-t^2/(2n) + o(1/n)]^n
\\
& \to e^{-t^2/2}
\end{align*}](img45.gif)
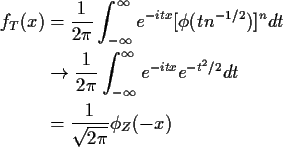
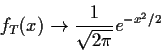
This proof of the central limit theorem is not terribly general
since it requires T to have a bounded continuous density. The usual central
limit theorem is a statement about cdfs not densities and is
In undergraduate courses we often teach the central limit theorem as
follows:
if
![]() are iid from a population with mean
are iid from a population with mean ![]() and standard
deviation
and standard
deviation ![]() then
then
![]() has approximately
a normal distribution. We also say that a Binomial(n,p) random variable
has approximately a
N(np,np(1-p)) distribution.
has approximately
a normal distribution. We also say that a Binomial(n,p) random variable
has approximately a
N(np,np(1-p)) distribution.
To make precise sense of these assertions we need to assign a meaning to
statements like ``X and Y have approximately the same distribution''.
The meaning we want to give is that X and Y have nearly the same cdf
but even here we need some care. If n is a large number is the
N(0,1/n) distribution close to the distribution of ![]() ? Is it
close to the
N(1/n,1/n) distribution? Is it close to the
? Is it
close to the
N(1/n,1/n) distribution? Is it close to the
![]() distribution? If
distribution? If
![]() is the distribution
of Xn close to that of
is the distribution
of Xn close to that of ![]() ?
?
The answer to these questions depends in part on how close close needs to be so it's a matter of definition. In practice the usual sort of approximation we want to make is to say that some random variable X, say, has nearly some continuous distribution, like N(0,1). In this case we must want to calculate probabilities like P(X>x) and know that this is nearly P(N(0,1) > x). The real difficulty arises in the case of discrete random variables; in this course we will not actually need to approximate a distribution by a discrete distribution.
When mathematicians say two things are close together they mean one of two things: either they can provide an upper bound on the distance between the two things or they are talking about taking a limit. In this course we do the latter.
Definition: A sequence of random variables Xn converges in
distribution to a random variable X if
Now let's go back to the questions I asked:
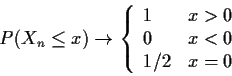
Here is the message you are supposed to take away from this discussion. You do distributional approximations by showing that a sequence of random variables Xn converges to some X. The limit distribution should be non-trivial, like say N(0,1). We don't say Xn is approximately N(1/n,1/n) but that n1/2 Xn converges to N(0,1) in distribution.