


Postscript version of these notes
STAT 350: Lecture 15
Reading: Chapter 7 sections 1, 2. Chpater 5 sections 11 and
12.
Extra Sum of Squares
Here is a more general version of the extra Sum of Squares method.
Consider two
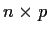 design matrices, X and X*. Suppose
that there is a
design matrices, X and X*. Suppose
that there is a
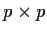 invertible matrix A such that
X=X* A.
invertible matrix A such that
X=X* A.
If we fit the model
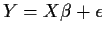 we get
we get
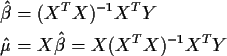
Fitting the model
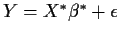 we get
we get
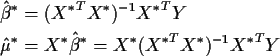
Now plug in X* A for X in 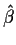 and
and 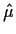 to get
to get
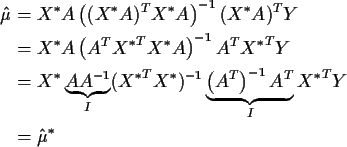
So X and X* lead to the same fitted vector.
Notice that
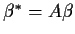 and
and
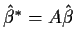 .
.
If X=X*A for some invertible A then
Now suppose that X=X*A but that A is not invertible
(for example X might have fewer columns than X*).
The idea is that in this case X describes a sub-model of that described
by X.
Example: The two sample problem.
where there are n1 rows of
![$[1 \quad 0]$](img14.gif) and n2 of
and n2 of
![$[0 \quad 1]$](img15.gif) .
.
where X is
 .
Then
.
Then
The model
is really
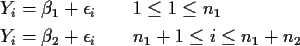
that is, it is the model for two samples of sizes n1 and n2
with means 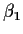 and
and 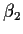 .
The model
.
The model
is just
that is, that the Yi are an iid sample from a single population.
We compare these two models to test
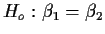 using
using
Summary: to compare two models with design matrices X
and X* we need
That is, we need the restricted model to be a special case of the full
model where we put some linear combinations of the 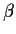 s equal to
constants. (The constants are usually 0.)
s equal to
constants. (The constants are usually 0.)
In our example consider the special case n1 = n2.
If we reparametrize the * model using
then we find
where
In this case we see that X is a submatrix of X**. This is why
the extra sum of squares principle can be used whenever the restricted
model is a special case of the full model, even if X is not a
submatrix of X*.
Another Extra Sum of Squares Example: two way layout
We have data Yi,j,k for i from 1 to I, j from 1 to J and k
from 1 to K where i labels the row effect, j labels the column effect
and k labels the replicate. When K is more than 1 we generally check for
interactions by comparing the additive model
to a saturated model in which the mean 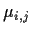 for the combination
i,j is unrestricted. Thus the full model is
for the combination
i,j is unrestricted. Thus the full model is
The additive model is not identifiable (that is, the design matrix is not
of full rank) unless some conditions are imposed on the row effects 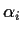 and the column effects
and the column effects 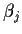 .
A common restriction imposed is that the effects
sum to 0; this restriction is then used to eliminate
.
A common restriction imposed is that the effects
sum to 0; this restriction is then used to eliminate 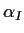 and
and 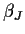 from the model equations. The resulting design matrix then has
1+(I-1)+(J-1) = I+J-1
columns and looks like
from the model equations. The resulting design matrix then has
1+(I-1)+(J-1) = I+J-1
columns and looks like
(There are K copies of the first row for the observations in population i=1,j=1,
then K copies of the row for observations in population i=1,j=2 and so on
till we get to j=J. Elimination of
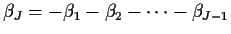 produces -1's in the J-1 columns corresponding to the
produces -1's in the J-1 columns corresponding to the 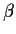 's. Then we move to
the JK rows corresponding to i=2 and so on with the last JK rows having
-1's in the
's. Then we move to
the JK rows corresponding to i=2 and so on with the last JK rows having
-1's in the 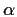 columns reflecting the identity
columns reflecting the identity
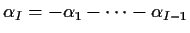 .)
.)
The full model is often reparametrized as
but the design matrix is actually much simpler for the first parameterization:
where there are K copies of the first row,
![$[1,0,\ldots,0]$](img45.gif) and
then K copies of
and
then K copies of
![$[0,1,0,\ldots,0]$](img46.gif) and so on. There are a total of IJ columns
and IJK rows.
and so on. There are a total of IJ columns
and IJK rows.
It is not hard to find a matrix A such that
For instance the first column of A will be all 1's since this corresponds to adding
the columns of
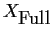 together and this produces a column of 1's which
is the first column of
together and this produces a column of 1's which
is the first column of
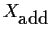 .
To produce the second column of
.
To produce the second column of
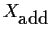 we have to add together the first I columns of
we have to add together the first I columns of
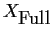 and then subtract
out the last I columns of
and then subtract
out the last I columns of
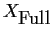 .
Thus the second column of A consists
of I 1's followed by I(J-2) 0's followed by I -1's.
.
Thus the second column of A consists
of I 1's followed by I(J-2) 0's followed by I -1's.



Richard Lockhart
1999-01-13
![]() design matrices, X and X*. Suppose
that there is a
design matrices, X and X*. Suppose
that there is a
![]() invertible matrix A such that
X=X* A.
invertible matrix A such that
X=X* A.
![]() we get
we get
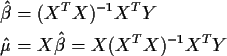
![]() we get
we get
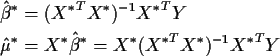
![]() and
and ![]() to get
to get
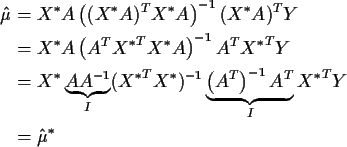
![]() and
and
![]() .
.
![\begin{displaymath}X^* =
\left[ \begin{array}{cc}
1 & 0
\\
1 & 0
\\
\vdots &...
... 0
\\
0 & 1
\\
\vdots & \vdots
\\
0 & 1
\end{array}\right]
\end{displaymath}](img13.gif)
![\begin{displaymath}X=\left[ \begin{array}{c}
1 \\ \vdots \\ 1 \end{array}\right]
\end{displaymath}](img16.gif)
![\begin{displaymath}X^* \left[\begin{array}{c} 1 \\ 1 \end{array}\right] = X
\end{displaymath}](img18.gif)
![]() using
using
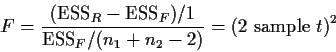
![\begin{displaymath}X^*\beta = X^{**} \left[ \begin{array}{c} \mu \\ \alpha \end{array} \right]
\end{displaymath}](img30.gif)
![\begin{displaymath}X^{**} = \left[ \begin{array}{cc}
1 & 1
\\
1 & 1
\\
\vdot...
...\\
1 & -1
\\
\vdots & \vdots
\\
1 & -1
\end{array} \right]
\end{displaymath}](img31.gif)
![\begin{displaymath}X_{\mbox{add}} = \left[\begin{array}{rrrcrrr}
1 & 1 & 0 & \cd...
...\
1 & -1 & -1 & \cdots & -1 & -1 & \cdots
\end{array}\right]
\end{displaymath}](img39.gif)
![\begin{displaymath}X_{\mbox{Full}} = \left[\begin{array}{rrrrr}
1 & 0 & 0 & \cd...
...\\
& & \vdots \\
0 & 0 & 0 & \cdots & 1
\end{array}\right]
\end{displaymath}](img44.gif)