Reading: Chapter 3, Chapter 9.
Model Assessment and Residual Analysis:
Recall that
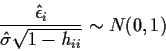
Critique: when the model is wrong a bad data point
can inflate
![]() leaving the internally studentized residual small.
leaving the internally studentized residual small.
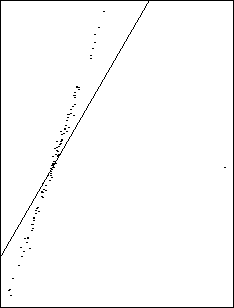
Suggestion:
But:
![]() must be compared to other residuals or
to
must be compared to other residuals or
to ![]() so we suggest Externally Studentized Residuals which are
also called Case Deleted Residuals:
so we suggest Externally Studentized Residuals which are
also called Case Deleted Residuals:
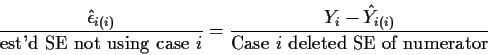
Apparent problem: If n=100 do I have to run SAS 100 times? NO.
FACT 1:
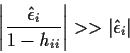
FACT 2:
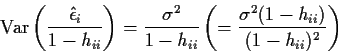
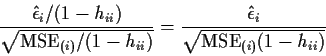
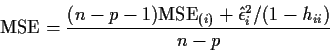
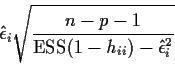
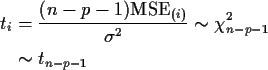
Cubic Fit:
| Year |
|
Internally | PRESS | Externally | Leverage |
| Studentized | Studentized | ||||
| 1975 | 1.17 | 0.59 | 1.54 | 0.56 | 0.24 |
| 1980 | -1.09 | -1.15 | -6.20 | -1.19 | 0.82 |
Note the influence of the leverage.
Note that edge observations (1980) have large leverage.
Quintic Fit:
| Year |
|
Internally | PRESS | Externally | Leverage |
| Studentized | Studentized | ||||
| 1978 | 0.82 | 1.79 | 1.43 | 3.48 | 0.43 |
| 1980 | 0.08 | 1.02 | 4.79 | 1.03 | 0.98 |
Notice 1978 residual is unacceptably large.
Notice 1980 leverage is huge.
Suppose X is the design matrix of a linear model and
that X1 is the design matrix of the linear model we get by imposing
some linear restrictions on the model using X. A good example is on
assignment 3 but here is another. Consider the one way layout,
also called the K sample problem. We have K samples from K
populations with means ![]() for
for
![]() .
Suppose the ith
sample size is n+i. This is a linear model, provided
we are able to assume that all the population variances are the same.
.
Suppose the ith
sample size is n+i. This is a linear model, provided
we are able to assume that all the population variances are the same.
The resulting design matrix is
![\begin{displaymath}X = \left[\begin{array}{rrrrr}
1 & 0 & 0 & \cdots & 0 \\
&...
...\\
& & \vdots \\
0 & 0 & 0 & \cdots & 1
\end{array}\right]
\end{displaymath}](img25.gif)
![\begin{displaymath}F=\frac{ [\sum (Y_{ij}-\bar{Y}_{\cdot\cdot})^2 -
\sum (Y_{i...
...t})^2]/(K-1)}{
\sum (Y_{ij}-\bar{Y}_{i\cdot})^2 /(\sum n_i-K)}
\end{displaymath}](img33.gif)
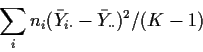
It is actually quite common to reparametrize the full model in such
a way that the null hypothesis of interest is of the form
![]() .
For the 1 way ANOVA there are two such reparametrizations in common use.
.
For the 1 way ANOVA there are two such reparametrizations in common use.
The first of these defines a grand mean parameter
![]() and individual ``effects''
and individual ``effects''
![]() .
This new
model has K+1 parameters apparently and the corresponding design
matrix, X1, would not have full rank; its rank would be K
although it would have K+1 columns. As such the matrix X1T X1
would be singular and we could not find unique least squares estimates.
The problem is that we have defined the parameters
in such a way that there is a linear restriction on them, namely,
.
This new
model has K+1 parameters apparently and the corresponding design
matrix, X1, would not have full rank; its rank would be K
although it would have K+1 columns. As such the matrix X1T X1
would be singular and we could not find unique least squares estimates.
The problem is that we have defined the parameters
in such a way that there is a linear restriction on them, namely,
![]() .
We get around this problem by dropping
.
We get around this problem by dropping ![]() and remembering in
our model equations that
and remembering in
our model equations that
![]() .
.
If you now write out the model equations with ![]() and the
and the
![]() as parameters you get the design matrix
as parameters you get the design matrix
![\begin{displaymath}X_2 = \left[\begin{array}{rrrrr}
1 & 1 & 0 & \cdots & 0 \\
...
...}{n_K} & \cdots & -\frac{n_{K-1}}{n_K}
\end{array}\right] \, .
\end{displaymath}](img43.gif)
Students will have seen this matrix in 330 in the case where all the
ni are the same and the fractions in the last nK rows of X2
are all equal to -1. Notice that the hypothesis
![]() is the same as
is the same as
![]() .
.
The other reparametrization is ``corner-point coding'' where we define
new parameters by
![]() and
and
![]() .
For
this parameterization the
null hypothesis of interest is
.
For
this parameterization the
null hypothesis of interest is
![]() .
The
design matrix is
.
The
design matrix is
![\begin{displaymath}X_3 = \left[\begin{array}{rrrrr}
1 & 0 & 0 & \cdots & 0 \\
...
... & \vdots \\
1 & 0 & 0 & \cdots & 1
\end{array}\right] \, .
\end{displaymath}](img48.gif)