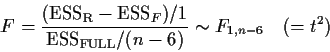Postscript version of these notes
STAT 350: Lecture 12
Reading: Chapter 7.
Extra Sum of Squares
Suppose we are fitting a model of the form
We can test the hypothesis
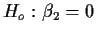 using the F test:
using the F test:
where p is the total number of columns of the design matrix
X=[X1 | X2 ] and
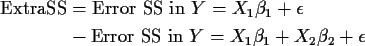
ANOVA tables
The calculations for the test above are usually recorded in an ANalysis Of
VAriance (ANOVA) table. Generally the design matrix will have a column of
ones and we adjust the entries in the table for the grand mean 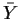 .
In this case we have
.
In this case we have
where X1 has p1 columns, X2 has p2 columns and there are
a total of 1+p1+p2 parameters in the parameter vector
We use the notation p=p1+p2 but you must be careful: don't memorize
formulas - learn to count columns. We decompose the data as
The components are mutually orthogonal so that we get the sum of squares
identity
which we normally put into an ANOVA table:
| Source |
Sum of Squares |
Degrees of Freedom |
| X1 |
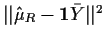 |
p1 |
| X2|X1 |
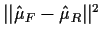 |
p2 |
| Error |
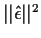 |
n-p-1 |
| Total (Corrected) |
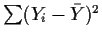 |
n-1 |
Typically we add a column of mean squares, always obtained by dividing
the SS column by the degrees of freedom column, a column of F statistics,
obtained by dividing the Mean Square by the MSE and a column of P values
obtained from software which computes F distribution tail areas.
In this table the notation X2|X1 means X2 adjusted
for
X1 or X2 after fitting X1.
Analysis of SAND / FIBRE / HARDNESS of plaster example
We regress Y, the hardness of a plaster sample on S, S2, F, F2
and SF. There are 5 factors so there are 25=32 possible submodels of
the full model
Many of these 32 models are not sensible, such as
or
The term
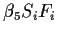 is an interaction of S and F. We
analyze the data as follows:
is an interaction of S and F. We
analyze the data as follows:
Q: Are the effects of S and F additive?
A: Test
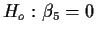 .
.
There are two methods to carry out such a test:
- 1.
- A t test
- 2.
- A F test.
Fact: the F test is equivalent to a two sided t
test.
The t test uses
This is exactly the same as the Lecture
10
formula since
and
xT(XTX)-1 x is the lower right hand corner entry in
(XTX)-1,
that is,
(XTX)-166.
The F test uses
Proof by example:
The Data
- Y = hardness of plaster. n=18 batches.
- S = sand content. Values used 0%, 15% 30%.
- F = fibre content. Values used 0%, 25% 50%.
- Factorial design with 2 replicates.
Sand Fibre Hardness Strength
0 0 61 34
0 0 63 16
15 0 67 36
15 0 69 19
30 0 65 28
...
``Full'' model
Fitted Models, ESS, df for error
Model for 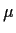 |
ESS |
Error df |
| Full |
81.264 |
12 |
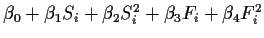 |
82.389 |
13 |
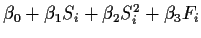 |
104.167 |
14 |
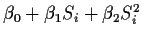 |
169.500 |
15 |
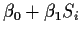 |
174.194 |
16 |
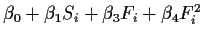 |
87.083 |
14 |
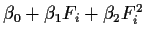 |
189.167 |
15 |
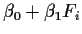 |
210.944 |
16 |
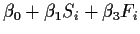 |
108.861 |
15 |
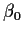 (empty model) (empty model) |
276.278 |
17 |
Hypothesis tests:
- 1.
- Quadratic terms needed?
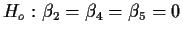 .
Extra SS = 108.861-81.264.
F=[ (108.861-81.264)/3]/[81.264/12]= 1.358.
Degrees of freedom are 3,12 so P=0.30, not significant.
.
Extra SS = 108.861-81.264.
F=[ (108.861-81.264)/3]/[81.264/12]= 1.358.
Degrees of freedom are 3,12 so P=0.30, not significant.
- 2.
- Linear terms needed? There are several possible F-tests.
- (a)
- Compare full model to empty model.
F=(276.278-81.264)/5/(81.264/12) =
5.76
so P is about .006.
- (b)
- Assume full model is now additive, linear model
Then
F=[(276.278-108.861)/2]/[108.861/15] = 11.53
and P is about 0.0009.
- (c)
- Use estimate of
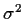 from full model but get extra SS from last comparison:
F=[(276.278-108.861)/2]/[81.264/12] = 12.36 for a P value of 0.001
from full model but get extra SS from last comparison:
F=[(276.278-108.861)/2]/[81.264/12] = 12.36 for a P value of 0.001
Conclusions
- Both Sand and Fibre influence Hardness.
- Linear terms in S and F are adequate.
You should also examine residual plots.
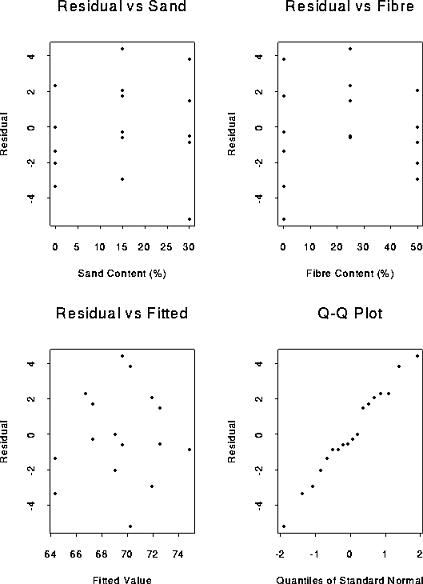
Here is a page of plots:
You will see that the plot of residual against fitted value suggests that we should
consider adding a quadratic term in Fibre:
The model
has ESS=87.083 on 14 degrees of freedom while the model
has ESS 108.861 on 15 degrees of freedom. The F statistic is
12*(108.861-87.083)/87.083 =3.00 with a corresponding P-value of roughly 0.10.
Thus the evidence that a quadratic term is needed is weak.



Richard Lockhart
1999-01-13
![\begin{displaymath}Y = [X_1 \vert X_2 ] \left[ \begin{array}{c}
\beta_1 \\ \hline \beta_2 \end{array}\right] + \epsilon
\end{displaymath}](img1.gif)
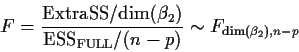
![]() .
In this case we have
.
In this case we have
![\begin{displaymath}\beta = \left[
\begin{array}{c} \beta_0 \\ \hline \beta_1 \\ \hline \beta_2 \end{array}\right]
\end{displaymath}](img7.gif)
![]() .
.
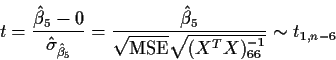
![\begin{displaymath}\beta_5 = \underbrace{[0,0,0,0,0,1]}_{x^T}\left[
\begin{array}{c} \beta_0 \\ \beta_1 \\ \vdots \\ \beta_5 \end{array}\right]
\end{displaymath}](img20.gif)