Reading: Chapter 7 Sections 1-3, 7 and 8.
Example:

Model:
![\begin{displaymath}\left[ \begin{array}{c} Y_1 \\ \vdots \\ Y_n \end{array}\righ...
...egin{array}{c} \beta_0 \\ \vdots \\ \beta_5 \end{array}\right]
\end{displaymath}](img3.gif)
Questions:
To answer these questions we test
Technique: we fit a sequence of models:
![\begin{displaymath}Y = \left[ {\bf 1} \vert X_1 \vert X_2 \vert X_3 \right]
\lef...
...3 \\ \beta_4 \\
\hline \beta_5 \end{array} \right]
+ \epsilon
\end{displaymath}](img13.gif)
The design matrices for the models a, b, c, d and e are given by
![\begin{eqnarray*}X_1 & = & X
\\
X_b & = & \left[{\bf 1} \vert X_1 \vert X_2 \ri...
...ft[{\bf 1} \vert X_2 \right]
\\
X_e & = & \left[{\bf 1} \right]
\end{eqnarray*}](img14.gif)
We can compare two models easily if one is a special case of the other, such as for example, when the design matrix of the first model is a submatrix of the second obtained by selecting subcolumns.
For example model (b) is a special case of (a), model (c) is a special case of (a) or (b) but models (c) and (d) are not comparable.
We consider the case of a design matrix X partitioned into two pieces
X1 and X2.
![\begin{align*}Y & = X\beta + \epsilon
\\
& =[ X_1 \vert X_2 ] \left[ \begin{arr...
...ray}\right]
+ \epsilon
\\
& = X_1 \beta_1 + X_2 \beta_2 + \epsilon
\end{align*}](img15.gif)
Dimensions:
![]() has p parameters.
has p parameters.
![]() has pi parameters with
p1 + p2 = p.
has pi parameters with
p1 + p2 = p.
To test
![]() we fit both the full and the reduced
models and get
we fit both the full and the reduced
models and get
![]()
where the subscript F refers to the full model and R to the reduced
model. This leads to the decomposition of the data vector Y into the sum
of three perpendicular vectors:
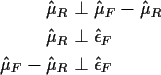
| Source | Sum of Squares | Degrees of Freedom |
| X2 |
|
p1 |
| X2|X1 |
|
p2 |
| Error |
|
n-p |
| Total (Unadjusted) | ||Y||2 | n |
In this table the notation X2|X1 means X2 adjusted for X1 or X2 after fitting X1.
This table can now be used to test
![]() by
computing
by
computing
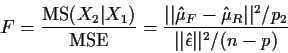
recall that
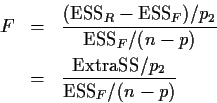
Remarks:
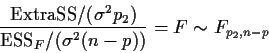
In the data set below the hardness of plaster is measured for each of 9 combinations of sand content and fibre content. Sand content was set at one of 3 levels as was fibre content and all possible combinations tried on two batches of plaster.
Here is an excerpt of the data:
Sand Fibre Hardness Strength
0 0 61 34
0 0 63 16
15 0 67 36
15 0 69 19
30 0 65 28
...
The complete data set is here.
I fit submodels of the following "Full" model:
| Model for |
Error Sum of Squares | Error df |
| Full | 81.264 | 12 |
|
|
82.389 | 13 |
|
|
104.167 | 14 |
|
|
169.500 | 15 |
|
|
174.194 | 16 |
|
|
87.083 | 14 |
|
|
189.167 | 15 |
|
|
210.944 | 16 |
|
|
108.861 | 15 |
I begin by asking whether the 2nd degree polynomial terms, that is,
those involving
![]() and
and ![]() need be included.
To do so I compare the top line with the model containing only
need be included.
To do so I compare the top line with the model containing only
![]() .
The extra SS is 108.861-81.264
on 3 degrees of freedom which gives a mean square of (108.861-81.264)/3=
9.199. The MSE is 81.264/12 = 6.772. This gives an F-statistic
of 9.199/6.772=1.358 on 3 numerator and 12 denominator degrees of freedom.
This gives a P-value of 0.30 which is not significant. We would then
delete the quadratic terms and consider the coefficients of S and F.
We have a choice between pretending that the last line in the table is
now the "Full" model and forming the F-statistics
(210.944-108.861)/(108.861/15) = 14.066 and (174.194-108.861)/(108.861/15)
= 9.002. The first is for testing
.
The extra SS is 108.861-81.264
on 3 degrees of freedom which gives a mean square of (108.861-81.264)/3=
9.199. The MSE is 81.264/12 = 6.772. This gives an F-statistic
of 9.199/6.772=1.358 on 3 numerator and 12 denominator degrees of freedom.
This gives a P-value of 0.30 which is not significant. We would then
delete the quadratic terms and consider the coefficients of S and F.
We have a choice between pretending that the last line in the table is
now the "Full" model and forming the F-statistics
(210.944-108.861)/(108.861/15) = 14.066 and (174.194-108.861)/(108.861/15)
= 9.002. The first is for testing
![]() and the second for
and the second for
![]() .
Each is on 1 and 15 degrees of freedom. The corresponding
P-values are 0.002 and 0.009. This are both highly significant and
we conclude that both Sand content and Fibre content have an impact
on hardness and that there is little reason to look for non-linear
impacts of the the two factors.
.
Each is on 1 and 15 degrees of freedom. The corresponding
P-values are 0.002 and 0.009. This are both highly significant and
we conclude that both Sand content and Fibre content have an impact
on hardness and that there is little reason to look for non-linear
impacts of the the two factors.
An alternative starting point would be to check first to see if the
interaction terms could be eliminated, that is, test the hypothesis
that ![]() .
This hypothesis can be tested either using the Fstatistic [(82.389-81.264)/1]/[12.264/12] = 0.166 or using the
t-statistic which is
.
This hypothesis can be tested either using the Fstatistic [(82.389-81.264)/1]/[12.264/12] = 0.166 or using the
t-statistic which is
![]() and which SAS calculates to be
-0.41. Note that
(-0.41)2 = 0.166 to within round-off error.
Algebraically F=t2. Note, too, that the t test can be made
one-sided while the F-test cannot.
and which SAS calculates to be
-0.41. Note that
(-0.41)2 = 0.166 to within round-off error.
Algebraically F=t2. Note, too, that the t test can be made
one-sided while the F-test cannot.